Mathematics

3 STEVIN.

Decimal Fractions

THE FIRST PART

Of the Definitions of the Dime.

THE FIRST DEFINITION

Dime is a kind of arithmetic, invented by the tenth progression, consisting in characters of ciphers, whereby a certain number is described and by which also all accounts which happen in human affairs are dispatched by whole numbers, without fractions or broken numbers.

Explication. Let the certain number be one thousand one hundred and eleven, described by the characters of ciphers thus 1111, in which it appears that each 1 is the 10th part of his precedent character 1; likewise in 2378 each unity of 8 is the tenth of each unity of 7, and so of all the others. But because it is convenient that the things whereof we would speak have names, and that this manner of computation is found by the consideration of such tenth or dime progression, that is that it consists therein entirely, as shall hereafter appear, we call this treatise fitly by the name of Dime, whereby all accounts happening in the affairs of man may be wrought and effected without fractions or broken numbers, as hereafter appears.

THE SECOND DEFINITION

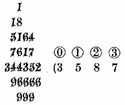
Every number propounded is called COMMENCEMENT, whose sign is thus

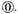
Explication. By example, a certain number is propounded of three hundred sixty-four: we call them the 364 commencements, described thus

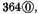
and so of all other like.

THE THIRD DEFINITION

And each tenth part of the unity of the COMMENCEMENT we call the PRIME, whose sign is thus

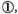and each tenth part of the unity of the prime we call the SECOND, whose sign is 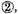and so of the other: each tenth part of the unity of the precedent sign, always in order one further.

Explication. As

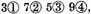
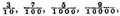
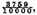
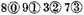
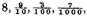
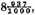
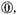
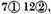
that is to say: 3 primes, 7 seconds, 5 thirds, 9 fourths, and so proceeding infinitely, but to speak of their value, you may note that according to this definition the said numbers are together and likewise are worth together and so of other like. 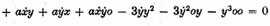Also you may understand that in this dime we use no fractions, and that the multitude of signs, except never exceed 9, as for example not but in their place for they value as much.

THE FOURTH DEFINITION

The numbers of the second and third definitions be foregoing are generally called DIME NUMBERS.

The End of the Definitions

THE SECOND PART OF THE DIME.

Of the Operation or Practice.

THE FIRST PROPOSITION: OF ADDITION

Dime numbers being given, how to add them to find their sum.

The Explication Propounded: There are 3 orders of dime numbers given, of which the first

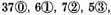
the second the third

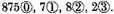
The Explication Required: We must find their total sum.

Construction. The numbers given must be placed in order as here adjoining, adding them in the vulgar manner of adding of whole numbers in this manner. The sum (by the first problem of our French Arithmetic²) is 941304, which are (that which the signs above the numbers do show)

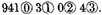
I say they are the sum required.

Demonstration. The

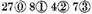
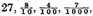
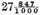
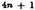
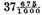
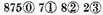
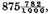
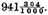
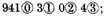
given make by the 3rd definition before together and by the same reason the Shall make and the will make which three numbers make by common addition of vulgar arithmetic But so much is the sum therefore it is the true sum to be demonstrated. Conclusion: Then dime numbers being given to be added, we have found their sum, which is the thing required.

Note that if in the number given there want some signs of their natural order, the place of the defectant shall be filled. As for example, let the numbers given be

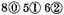
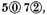
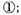
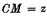
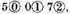
and in which the latter wanted the sign of in the place thereof shall be put. Take then for that latter number given adding them in this sort.

This advertisement shall also serve in the three following propositions, wherein the order of the derailing figures must be supplied, as was done in the former example.

THE SECOND PROPOSITION: OF SUBTRACTION

A dime number being given to subtract, another less dime number given: out of the same to find their rest.

Explication Propounded: Be the numbers given

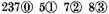
and

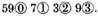
The Explication Required: To find their rest.

Construction. The numbers given shall be placed in this sort, subtracting according to vulgar manner of subtraction of whole numbers, thus.

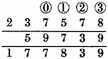
The rest is 177839, which values as the signs over them do denote

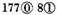
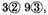
I affirm the same to be the rest required.

Demonstration. The

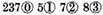
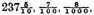
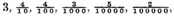
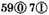
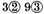
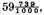
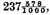
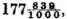
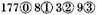
make (by the third definition of this Dime) together and by the same reason the value which subtracted from there rests but so much doth value; that is then the true rest which should be made manifest.

Conclusion. A dime being given, to subtract it out of another dime number, and to know the rest, which we have found.

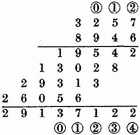
THE THIRD PROPOSITION: OF MULTIPLICATION

A dime number being given to be multiplied, and a multiplicator given: to find their product.

The Explication Propounded: Be the number to be multiplied

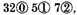
and the multiplicator

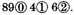
The Explication Required: To find the product.

Construction. The given numbers are to be placed as here is shown, multiplying according to the vulgar manner of multiplcation by whole numbers, in this manner, giving the product 29137122. Now to know how much they value, join the two last signs together as the one

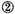
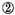
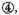
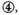
and the other also, which together make and say that the last sign of the product shall be which being known, all the rest are also known by their continued order. So that the product required is

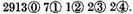
Demonstration. The number given to be multiplied,

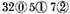
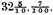
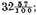
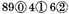
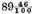
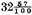
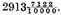
(as appears by the third definition of this Dime), together and by the same reason the multiplicator value by the same, the said multiplied gives the product But it also values

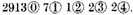
It is then the true product, which we were to demonstrate. But to show why

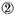
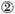
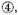
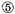
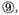
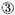
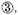
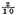
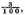
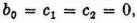
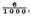
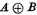
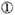
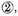
multiplied by gives the product which is the sum of their numbers, also why by produces and why by produces etc., let us take and which (by the third definition of this Dime) are their product is which value by the said third definition multiplying then by the product is namely a sign compounded of the sum of the numbers of the signs given.

Conclusion. A dime number to multiply and to be multiplied being given, we have found the product, as we ought.

Note: If the latter sign of the number to be multiplied be unequal to the latter sign of the multiplicator, as, for example, the one

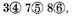the other 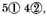they shall be handled as aforesaid, and the disposition thereof shall be thus.

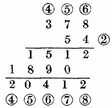
THE FOURTH PROPOSITION: OF DIVISION

A dime number for the dividend and divisor being given: to find the quotient.

Explication Proposed: Let the number for the dividend be

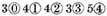
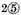
and the divisor

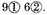
Explication Required: To find their quotient.

Construction. The numbers given divided (omitting the signs) according to the vulgar manner of dividing of whole numbers, gives the quotient 3587; now to know what they value, the latter sign of the divisor

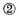
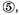
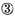
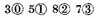
must be subtracted from the latter sign of the dividend, which is rests for the latter are also manifest by their continued order, thus are the quotient required.

Demonstration. The number dividend given

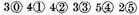
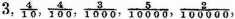
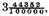
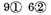
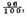
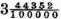
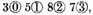
makes (by the third definition of this Dime) together and by the same reason the divisor values by which being divided, gives the quotient but the said quotient values therefore it is the true quotient to be demonstrated.

Conclusion. A dime number being given for the dividend and divisor, we have found the quotient required.

Note: If the divisor’s signs be higher than the signs of the dividend, there may be as many such ciphers 0 joined to the dividend as you will, or as many as shall be necessary: as for example,

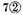are to be divided by 1 place after the 7 certain thus 7000, dividing them as afore said, and in this sort it gives for the quotient

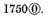
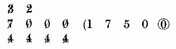
It happens also sometimes that the quotient cannot be expressed by whole numbers, as

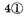
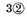
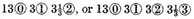
divided by in this sort, whereby appears that there will infinitely come 3’s, and in such a case you may come so near as the thing requires, omitting the remainder. It is true, that etc. shall be the perfect quotient required. But our invention in this Dime is to work all by whole numbers. For seeing that in any affairs men reckon not of the thousandth part of a mite, es, grain, etc., as the like is also used of the principal geometers and astronomers in computations of great consequence, as Ptolemy and Johannes Montaregio,³ have not described their tables of arcs, chords, or sines in extreme perfection (as possibly they might have done by multinomial numbers), because that imperfection (considering the scope and end of those tables) is more convenient than such perfection.

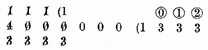
Note 2. The extraction of all kinds of roots may also be made by these dime numbers; as, for example, to extract the square root of

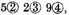
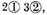
which is performed in the vulgar manner of extraction in this sort, and the root shall be for the moiety or half of the latter sign of the numbers given is always the latter sign of the root; wherefore, if the latter sign given were of a number impair, the sign of the next following shall be added, and then it shall be a number pair; and then extract the root as before. Likewise in the extraction of the cubic root, the third part of the latter sign given shall be always the sign of the root; and so of all other kinds of roots.

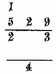
THE END OF THE DIME

¹ P. Luckey, Die Rechenkunst bei [figure table]

b. (Steiner, Wiesbaden, 1951).

²L’Arithmétique de Simon Stevin de Bruges (Leyden, 1585); see Stevin, The principal works (Swets-Zeitlinger, Amsterdam), vol. IIB (1958). Problem I (p. 81) is: "Given two arithmetical integer numbers. Find their sum."

³ Johannes Montaregio (1436–1476) is best known under his latinized name, Johannes Regiomontanus. This craftsman, humanist, astronomer, and mathematician of Nuremberg influenced the development of trigonometry by means of his widely used book De triangulis omnimodis (written c. 1464, printed in Nuremberg in 1533). The sines, for Regiomontanus as well as for Stevin, were half chords; see our note to the following text on Napier and Selection III.2.