The Number of Primes Is Infinite

Name: The Number of Primes Is Infinite - The Number of Primes Is Infinite
Author: Euclid

Euclid

Prime numbers are more than any assigned multitude of prime numbers.

Let A, B, C be the assigned prime numbers; I say that there are more prime numbers than A, B, C.

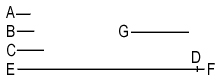
For let the least number measured by A, B, C be taken, and let it be DE; let the unit DF be added to DE.

Then EF is either prime or not.

First, let it be prime; then the prime numbers A, B, C, EF have been found, which are more than A, B, C.

Next let EF not be prime; therefore it is measured by some prime number. [VII. 31]

Let it be measured by the prime number G.

I say that G is not the same with any of the numbers A, B, C.

For, if possible, let it be so. [p.21]

Now A, B, C measure DE; therefore G also will measure DE.

But it also measures EF.

Therefore G, being a number, will measure the remainder, the unit DF: which is absurd.

Therefore G is not the same with any of the numbers A, B, C.

And by hypothesis it is prime.

Therefore the prime numbers A, B, C, G have been found which are more than the assigned multitude of A, B, C. Q.E.D.

Related Resources

Euclid
Life of Euclid

Download Options

Title: The Number of Primes Is Infinite

Select an option:

*Note: A download may not start for up to 60 seconds.

Email Options

Title: The Number of Primes Is Infinite

Select an option:

Email addres:

*Note: It may take up to 60 seconds for for the email to be generated.

Chicago: Euclid, The Number of Primes Is Infinite in A Source Book in Greek Science, ed. Morris R. Cohen and I. E. Drabkin (Cambridge, MA: Harvard University Press, 1966), 20–21. Original Sources, accessed November 23, 2024, http://originalsources.com/Document.aspx?DocID=D34J15CMJYNWP8J.

MLA: Euclid. The Number of Primes Is Infinite, in A Source Book in Greek Science, edited by Morris R. Cohen and I. E. Drabkin, Cambridge, MA, Harvard University Press, 1966, pp. 20–21. Original Sources. 23 Nov. 2024. http://originalsources.com/Document.aspx?DocID=D34J15CMJYNWP8J.

Harvard: Euclid, The Number of Primes Is Infinite. cited in 1966, A Source Book in Greek Science, ed. , Harvard University Press, Cambridge, MA, pp.20–21. Original Sources, retrieved 23 November 2024, from http://originalsources.com/Document.aspx?DocID=D34J15CMJYNWP8J.