The Internal Constitution of the Stars
Arthur Stanley Eddington
(Nature 106, 14–20 [1920])
LAST YEAR at Bournemouth we listened to a proposal from the President of the Association to bore a hole in the crust of the earth and discover the conditions deep down below the surface. This proposal may remind us that the most secret places of Nature are, perhaps, not 10 to the nth miles above our heads, but 10 miles below our feet. In the last five years the outward march of astronomical discovery has been rapid, and the most remote worlds are now scarcely safe from its inquisition. By the work of H. Shapley the globular clusters, which are found to be at distances scarcely dreamt of hitherto, have been explored, and our knowledge of them is in some respects more complete than that of the local aggregation of stars which includes the sun. Distance lends not enchantment, but precision, to the view. Moreover, theoretical researches of Einstein and Weyl make it probable that the space which remains beyond is not illimitable; not merely the material universe, but also space itself, is perhaps finite; and the explorer must one day stay his conquering march for lack of fresh realms to invade. But to-day let us turn our thoughts inwards to that other region of mystery—a region cut off by more substantial barriers, for, contrary to many anticipations, even the discovery of the fourth dimension has not enabled us to get at the inside of a body. Science has material and non-material appliances to bore into the interior, and I have chosen to devote this address to what may be described as analytical boring devices—absit omen!
The analytical appliance is delicate at present, and, I fear, would make little headway against the solid crust of the earth. Instead of letting it blunt itself against the rocks, let us look round for something easier to penetrate. The sun? Well, perhaps. Many have struggled to penetrate the mystery of the interior of the sun; but the difficulties are great, for its substance is denser than water. It may not be quite so bad as Biron makes out in "Love’s Labour’s Lost":
The heaven’s glorious sun That will not be deep-search’d with saucy looks: Small have continual plodders ever won Save base authority from others’ books.
But it is far better if we can deal with matter in that state known as a perfect gas, which charms away difficulties as by magic. Where shall it be found?
A few years ago we should have been puzzled to say where, except perhaps in certain nebulæ; but now it is known that abundant material of this kind awaits investigation. Stars in a truly gaseous state exist in great numbers, although at first sight they are scarcely to be discriminated from dense stars like our sun. Not only so, but the gaseous stars are the most powerful light-givers, so that they force themselves on our attention. Many of the familiar stars are of this kind—Aldebaran, Canopus, Arcturus, Antares; and it would be safe to say that three-quarters of the naked-eye stars are in this diffuse state. This remarkable condition has been made known through the researches of H. N. Russell (Nature 93, 227, 252, 281) and E. Hertzsprung; the way in which their conclusions, which ran counter to the prevailing thought of the time, have been substantiated on all sides by overwhelming evidence is the outstanding feature of recent progress in stellar astronomy.
The diffuse gaseous stars are called giants, and the dense stars dwarfs. During the life of a star there is presumably a gradual increase of density through contraction, so that these terms distinguish the earlier and later stages of stellar history. It appears that a star begins its effective life as a giant of comparatively low temperature—a red or M-type star. As this diffuse mass of gas contracts its temperature must rise, a conclusion long ago pointed out by Homer Lane. The rise continues until the star becomes too dense, and ceases to behave as a perfect gas. A maximum temperature is attained, depending on the mass, after which the star, which has now become a dwarf, cools and further contracts. Thus each temperature-level is passed through twice, once in an ascending and once in a descending stage—once as a giant, once as a dwarf. Temperature plays so predominant a part in the usual spectral classification that the ascending and descending stars were not originally discriminated, and the customary classification led to some perplexities. The separation of the two series was discovered through their great difference in luminosity, particularly striking in the case of the red and yellow stars, where the two stages fall widely apart in the star’s history. The bloated giant has a far larger surface than the compact dwarf, and gives correspondingly greater light. The distinction was also revealed by direct determinations of stellar densities, which are possible in the case of eclipsing variables like Algol. Finally, Adams and Kohlschütter have set the seal on this discussion by showing that there are actual spectral differences between the ascending and descending stars at the same temperature-level, which are conspicuous enough when they are looked for.
Perhaps we should not too hastily assume that the direction of evolution is necessarily in the order of increasing density, in view of our ignorance of the origin of a star’s heat, to which I must allude later. But, at any rate, it is a great advance to have disentangled what is the true order of continuous increase of density, which was hidden by superficial resemblances.
The giant stars, representing the first half of a star’s life, are taken as material for our first boring experiment. Probably, measured in time, this stage corresponds to much less than half the life, for here it is the ascent which is easy and the way down is long and slow. Let us try to picture the conditions inside a giant star. We need not dwell on the vast dimensions—a mass like that of the sun, but swollen to much greater volume on account of the low density, often below that of our own atmosphere. It is the star as a storehouse of heat which especially engages our attention. In the hot bodies familiar to us the heat consists in the energy of motion of the ultimate particles, flying at great speeds hither and thither. So, too, in the stars a great store of heat exists in this form; but a new feature arises. A large proportion, sometimes more than half the total heat, consists of imprisoned radiant energy—æther-waves travelling in all directions trying to break through the material which encages them. The star is like a sieve, which can retain them only temporarily; they are turned aside, scattered, absorbed for a moment, and flung out again in a new direction. An element of energy may thread the maze for hundreds of years before it attains the freedom of outer space. Nevertheless, the sieve leaks, and a steady stream permeates outwards, supplying the light and heat which the star radiates all round.
That some æthereal heat as well as material heat exists in any hot body would naturally be admitted; but the point on which we have here to lay stress is that in the stars, particularly in the giant stars, the æthereal portion rises to an importance which quite transcends our ordinary experience, so that we are confronted with a new type of problem. In a red-hot mass of iron the æthereal energy constitutes less than a billionth part of the whole; but in the tussle between matter and æther the æther gains a larger and larger proportion of the energy as the temperature rises. This change in proportion is rapid, the æthereal energy increasing rigorously as the fourth power of the temperature, and the material energy roughly as the first power. But even at the temperature of some millions of degrees attained inside the stars there would still remain a great disproportion; and it is the low density of material, and accordingly the reduced material energy per unit volume in the giant stars, which wipes out the last few powers of 10. In all the giant stars known to us, widely as they differ from one another, the conditions are just reached at which these two varieties of heat-energy have attained a rough equality; at any rate, one cannot be neglected compared with the other. Theoretically there could be conditions in which the disproportion was reversed and the æthereal far outweighed the material energy; but we do not find them in the stars. It is as though the stars had been measured out—that their sizes had been determined—with a view to this balance of power; and one cannot refrain from attributing to this condition a deep significance in the evolution of the cosmos into separate stars.
To recapitulate. We are acquainted with heat in two forms—the energy of motion of material atoms and the energy of æther waves. In familiar hot bodies the second form exists only in insignificant quantities. In the giant stars the two forms are present in more or less equal proportions. That is the new feature of the problem.
On account of this new aspect of the problem the first attempts to penetrate the interior of a star are now seen to need correction. In saying this we do not depreciate the great importance of the early researches of Lane, Ritter, Emden, and others, which not only pointed the way for us to follow, but also achieved conclusions of permanent value. One of the first questions they had to consider was by what means the heat radiated into space was brought up to the surface from the low level where it was stored. They imagined a bodily transfer of the hot material to the surface by currents of convection, as in our own atmosphere. But actually the problem is, not how the heat can be brought to the surface, but how the heat in the interior can be held back sufficiently—how it can be barred in and the leakage reduced to the comparatively small radiation emitted by the stars. Smaller bodies have to manufacture the radiant heat which they emit, living from hand to mouth; the giant stars merely leak radiant heat from their store. I have put that much too crudely; but perhaps it suggests the general idea.
The recognition of æthereal energy necessitates a twofold modification in the calculations. In the first place, it abolishes the supposed convection currents; and the type of equilibrium is that known as radiative instead of convective. This change was first suggested by R. A. Sampson so long ago as 1894. The detailed theory of radiative equilibrium is particularly associated with K. Schwarzschild, who applied it to the sun’s atmosphere. It is perhaps still uncertain whether it holds strictly for the atmospheric layers, but the arguments for its validity in the interior of a star are far more cogent. Secondly, the outflowing stream of æthereal energy is powerful enough to exert a direct mechanical effect on the equilibrium of a star. It is as though a strong wind were rushing outwards. In fact, we may fairly say that the stream of radiant energy is a wind; for though æther waves are not usually classed as material, they have the chief mechanical properties of matter, viz. mass and momentum. This wind distends the star and relieves the pressure on the inner parts. The pressure on the gas in the interior is not the full weight of the superincumbent columns, because that weight is partially borne by the force of the escaping æther waves beating their way out. This force of radiation-pressure, as it is called, makes an important difference in the formulation of the conditions for equilibrium of a star.
Having revised the theoretical investigations in accordance with these considerations (Astrophysical Journal 48, 205), we are in a position to deduce some definite numerical results. On the observational side we have fairly satisfactory knowledge of the masses and densities of the stars and of the total radiation emitted by them; this knowledge is partly individual and partly statistical. The theoretical analysis connects these observational data on the one hand with the physical properties of the material inside the star on the other. We can thus find certain information as to the inner material, as though we had actually bored a hole. So far as can be judged, there are only two physical properties of the material which can concern us—always provided that it is sufficiently rarefied to behave as a perfect gas—viz. the average molecular weight and the transparency or permeability to radiant energy. In connecting these two unknowns with the quantities given directly by astronomical observation we depend entirely on the well-tried principles of conservation of momentum and the second law of thermodynamics. If any element of speculation remains in this method of investigation, I think it is no more than is inseparable from every kind of theoretical advance.
We have, then, on one side the mass, density, and output of heat, quantities as to which we have observational knowledge; on the other side, molecular weight and transparency, quantities which we want to discover.
To find the transparency of stellar material to the radiation traversing it is of particular interest, because it links on this astronomical inquiry to physical investigations now being carried on in the laboratory, and to some extent it extends those investigations to conditions unattainable on the earth. At high temperatures the æther waves are mainly of very short wave-length, and in the stars we are dealing mainly with radiation of wave-length 3 to 30 Ångström units, which might be described as very soft X-rays. It is interesting, therefore, to compare the results with the absorption of the harder X-rays dealt with by physicists. To obtain an exact measure of this absorption in the stars we have to assume a value of the molecular weight; but fortunately the extreme range possible for the molecular weight gives fairly narrow limits for the absorption. The average weight of the ultimate independent particles in a star is probably rather low, because in the conditions prevailing there the atoms would be strongly ionised; that is to say, many of the outer electrons of the system of the atom would be broken off; and as each of these free electrons counts as an independent molecule for present purposes, this brings down the average weight. In the extreme case (probably not reached in a star) when the whole of the electrons outside the nucleus are detached the average weight comes down to about 2, whatever the material, because the number of electrons is about half the atomic weight for all the elements (except hydrogen). We may, then, safely take 2 as the extreme lower limit. For an upper limit we might perhaps take 200; but to avoid controversy we shall be generous and merely assume that the molecular weight is not greater than—infinity. Here is the result:
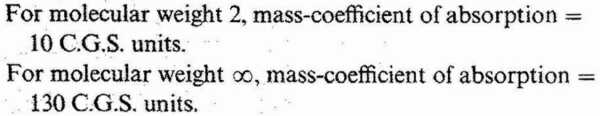
The true value, then, must be between 10 and 130. Partly from thermodynamical considerations, and partly from further comparisons of astronomical observation with theory, the most likely value seems to be about 35 C.G.S. units, corresponding to molecular weight 3.5.
Now this is of the same order of magnitude as the absorption of X-rays measured in the laboratory. I think the result is in itself of some interest, that in such widely different investigations we should approach the same kind of value of the opacity of matter to radiation. The penetrating power of the radiation in the star is much like that of X-rays; more than half is absorbed in a path of 20 cm. at atmospheric density. Incidentally, this very high opacity explains why a star is so nearly heat-tight, and can store vast supplies of heat with comparatively little leakage.
So far this agrees with what might have been anticipated; but there is another conclusion which physicists would probably not have foreseen. The giant series comprises stars differing widely in their densities and temperatures, those at one end of the series being on the average about ten times hotter throughout than those at the other end. By the present investigation we can compare directly the opacity of the hottest stars with that of the coolest. The rather surprising result emerges that the opacity is the same for all; at any rate, there is no difference large enough for us to detect. There seems no room for doubt that at these high temperatures the absorption-coefficient is approaching a limiting value, so that over a wide range it remains practically constant. With regard to this constancy, it is to be noted that the temperature is concerned twice over: it determines the character and wave-length of the radiation to be absorbed, as well as the physical condition of the material which is absorbing. From the experimental knowledge of X-rays we should have expected the absorption to vary very rapidly with the wave-length, and therefore with the temperature. It is surprising, therefore, to find a nearly constant value.
The result becomes a little less mysterious when we consider more closely the nature of absorption. Absorption is not a continuous process, and after an atom has absorbed its quantum it is put out of action for a time until it can recover its original state. We know very little of what determines the rate of recovery of the atom, but it seems clear that there is a limit to the amount of absorption that can be performed by an atom in a given time. When that limit is reached no increase in the intensity of the incident radiation will lead to any more absorption. There is, in fact, a saturation effect. In the laboratory experiments the radiation used is extremely weak; the atom is practically never caught unprepared, and the absorption is proportional to the incident radiation. But in the stars the radiation is very intense and the saturation effect comes in.
Even granting that the problem of absorption in the stars involves this saturation effect, which does not affect laboratory experiments, it is not very easy to understand theoretically how the various conditions combine to give a constant absorption-coefficient independent of temperature and wave-length. But the astronomical results seem conclusive. Perhaps the most hopeful suggestion is one made to me a few years ago by C. G. Barkla. He suggested that the capacity of the stars may depend mainly on scattering rather than on true atomic absorption. In that case the constancy has a simple explanation, for it is known that the coefficient of scattering (unlike true absorption) approaches a definite constant value for radiation of short wave-length. The value, moreover, is independent of the material. Further, scattering is a continuous process, and there is no likelihood of any saturation effect; thus for very intense streams of radiation its value is maintained, whilst the true absorption may sink to comparative insignificance. The difficulty in this suggestion is a numerical discrepancy between the known theoretical scattering and the values already given as deduced from the stars. The theoretical coefficient is only 0.2 compared with the observed value 10 to 130. Barkla further pointed out that the waves here concerned are not short enough to give the ideal coefficient; they would be scattered more powerfully, because under their influence the electrons in any atom would all vibrate in the same phase instead of in haphazard phases. This might help to bridge the gap, but not sufficiently. It must be remembered that many of the electrons have broken loose from the atom and do not contribute to the increase.1 Making all allowances for uncertainties in the data, it seems clear that the astronomical opacity is definitely higher than the theoretical scattering. Very recently, however, a new possibility has opened up which may possibly effect a reconciliation. Later in the address I shall refer to it again.
Astronomers must watch with deep interest the investigations of these short waves, which are being pursued in the laboratory, as well as the study of the conditions of ionisation by both experimental and theoretical physics, and I am glad of the opportunity of bringing before those who deal with these problems the astronomical bearing of their work.
I can allude only very briefly to the purely astronomical results which follow from this investigation (Monthly Notices 77, 16, 596, 79, 2); it is here that the best opportunity occurs for checking the theory by comparison with observation, and for finding out in what respects it may be deficient. Unfortunately, the observational data are generally not very precise, and the test is not so stringent as we could wish. It turns out that (the opacity being constant) the total radiation of a giant star should be a function of its mass only, independent of its temperature or state of diffuseness. The total radiation (which is measured roughly by the luminosity) of any one star thus remains constant during the whole giant stage of its history. This agrees with the fundamental feature, pointed out by Russell in introducing the giant and dwarf hypothesis, that giant stars of every spectral type have nearly the same luminosity. From the range of luminosity of these stars it is now possible to find their range of mass. The masses are remarkably alike—a fact already suggested by work on double stars. Limits of mass in the ratio 3:1 would cover the great majority of the giant stars. Somewhat tentatively we are able to extend the investigation to dwarf stars, taking account of the deviations of dense gas from the ideal laws and using our own sun to supply a determination of the unknown constant involved. We can calculate the maximum temperature reached by different masses; for example, a star must have at least 1/7 the mass of the sun in order to reach the lowest spectral type, M; and in order to reach the hottest type, B, it must be at least 2½ times as massive as the sun. Happily for the theory, no star has yet been found with a mass less than 1/7th of the sun’s; and it is a well-known fact, discovered from the study of spectroscopic binaries, that the masses of the B stars are large compared with those of other types. Again, it is possible to calculate the difference of brightness of the giant and dwarf stars of type M, i.e. at the beginning and end of their career; the result agrees closely with the observed difference. In the case of a class of variable stars in which the light changes seem to depend on a mechanical pulsation of the star, the knowledge we have obtained of the internal conditions enables us to predict the period of pulsation within narrow limits. For example, for δ Cephei, the best-known star of this kind, the theoretical period is between four and ten days, and the actual period is 51/3 days. Corresponding agreement is found in all the other cases tested.
Our observational knowledge of the things here discussed is chiefly of a rather vague kind, and we can scarcely claim more than a general agreement of theory and observation. What we have been able to do in the way of tests is to offer the theory a considerable number of opportunities to "make a fool of itself," and so far it has not fallen into our traps. When the theory tells us that a star having the mass of the sun will at one stage in its career reach a maximum effective temperature of 9,000° (the sun’s effective temperature being 6,000°) we cannot do much in the way of checking it; but an erroneous theory might well have said that the maximum temperature was 20,000° (hotter than any known star), in which case we should have detected its error. If we cannot feel confident that the answers of the theory are true, it must be admitted that it has shown some discretion in lying without being found out.
It would not be surprising if individual stars occasionally depart considerably from the calculated results, because at present no serious attempt has been made to take into account rotation, which may modify the conditions when sufficiently rapid. That appears to be the next step needed for a more exact study of the question.
Probably the greatest need of stellar astronomy at the present day, in order to make sure that our theoretical deductions are starting on the right lines, is some means of measuring the apparent angular diameters of stars. At present we can calculate them approximately from theory, but there is no observational check. We believe we know with fair accuracy the apparent surface brightness corresponding to each spectral type; then all that is necessary is to divide the total apparent brightness by this surface brightness, and the result is the angular area subtended by the star. The unknown distance is not involved, because surface brightness is independent of distance. Thus the estimation of the angular diameter of any star seems to be a very simple matter. For instance, the star with the greatest apparent diameter is almost certainly Betelgeuse, diameter 0.051″. Next to it comes Antares, 0.043″. Other examples are Aldebaran 0.022″, Arcturus 0.020″, Pollux 0.013″. Sirius comes rather low down with diameter 0.007″. The following table may be of interest as showing the angular diameters in seconds of are expected for stars of various types and visual magnitudes:

However confidently we may believe in these values, it would be an immense advantage to have this first step in our deductions placed beyond doubt. If the direct measurement of these diameters could be made with any accuracy it would make a wonderfully rapid advance in our knowledge. The prospects of accomplishing some part of this task are now quite hopeful. We have learnt with great interest this year that work is being carried out by interferometer methods with the 100-in. reflector at Mount Wilson, and the results are most promising. At present the method has been applied only to measuring the separation of close double stars, but there seems to be no doubt that an angular diameter of 0.05″ is well within reach. Although the great mirror is used for convenience, the interferometer method does not in principle require great apertures, but rather two small apertures widely separated, as in a range-finder. Prof. Hale has stated, moreover, that successful results were obtained on nights of poor seeing. Perhaps it would be unsafe to assume that "poor seeing" at Mount Wilson means quite the same thing as it does for us, and I anticipate that atmospheric disturbance will ultimately set the limit to what can be accomplished. But even if we have to send special expeditions to the top of one of the highest mountains in the world, the attack on this far-reaching problem must not be allowed to languish.
I spoke earlier of the radiation-pressure exerted by the outflowing heat, which has an important effect on the equilibrium of a star. It is quite easy to calculate what proportion of the weight of the material is supported in this way; it depends on neither the density nor the opacity, but solely on the star’s total mass and on the molecular weight. No astronomical data are needed; the calculation involves only fundamental physical constants found by laboratory researches. Here are the figures, first for average molecular weight 3.0:

For molecular weight 5.0 the corresponding fractions are 0.182 and 0.645.
The molecular weight can scarcely go beyond this range,2 and for the conclusions I am about to draw it does not much matter which limit we take. Probably 90 per cent. of the giant stars have masses between ½ and 5 times the sun’s, and we see that this is just the range in which radiation-pressure rises from unimportance to importance. It seems clear that a globe of gas of larger mass, in which radiation-pressure and gravitation are nearly balancing, would be likely to be unstable. The condition may not be strictly unstable in itself, but a small rotation or perturbation would make it so. It may therefore be conjectured that, if nebulous material began to concentrate into a mass much greater than five times the sun’s, it would probably break up, and continue to redivide until more stable masses resulted. Above the upper limit the chances of survival are small; when the lower limit is approached the danger has practically disappeared, and there is little likelihood of any further breaking-up. Thus the final masses are left distributed almost entirely between the limits given. To put the matter slightly differently, we are able to predict from general principles that the material of the stellar universe will aggregate primarily into masses chiefly lying between 1033 and 1034 grams; and this is just the magnitude of the masses of the stars according to astronomical observation.3
This study of the radiation and internal conditions of a star brings forward very pressingly a problem often debated in this Section: What is the source of the heat which the sun and stars are continually squandering? The answer given is almost unanimous—that it is obtained from the gravitational energy converted as the star steadily contracts. But almost as unanimously this answer is ignored in its practical consequences. Lord Kelvin showed that this hypothesis, due to Helmholtz, necessarily dates the birth of the sun about 20,000,000 years ago; and he made strenuous efforts to induce geologists and biologists to accommodate their demands to this time-scale. I do not think they proved altogether tractable. But it is among his own colleagues, physicists and astronomers, that the most outrageous violations of this limit have prevailed. I need only refer to Sir George Darwin’s theory of the earth-moon system, to the present Lord Rayleigh’s determination of the age of terrestrial rocks from occluded helium, and to all modern discussions of the statistical equilibrium of the stellar system. No one seems to have any hesitation, if it suits him, in carrying back the history of the earth long before the supposed date of formation of the solar system; and, in some cases at least, this appears to be justified by experimental evidence which it is difficult to dispute. Lord Kelvin’s date of the creation of the sun is treated with no more respect than Archbishop Ussher’s.
The serious consequences of this contraction hypothesis are particularly prominent in the case of giant stars, for the giants are prodigal with their heat and radiate at least a hundred times as fast as the sun. The supply of energy which suffices to maintain the sun for 10,000,000 years would be squandered by a giant star in less than 100,000 years. The whole evolution in the giant stage would have to be very rapid. In 18,000 years at the most a typical star must pass from the initial M stage to type G. In 80,000 years it has reached type A, near the top of the scale, and is about to start on the downward path. Even these figures are probably very much over-estimated.4 Most of the naked-eye stars are still in the giant stage. Dare we believe that they were all formed within the last 80,000 years? The telescope reveals to us objects remote not only in distance, but also in time. We can turn it on a globular cluster and behold what was passing 20,000, 50,000, even 200,000 years ago unfortunately not all in the same cluster, but in different clusters representing different epochs of the past. As Shapley has pointed out, the verdict appears to be "no change." This is perhaps not conclusive, because it does not follow that individual stars have suffered no change in the interval; but it is difficult to resist the impression that the evolution of the stellar universe proceeds at a slow, majestic pace, with respect to which these periods of time are insignificant.
There is another line of astronomical evidence which appears to show more definitely that the evolution of the stars proceeds far more slowly than the contraction hypothesis allows; and perhaps it may ultimately enable us to measure the true rate of progress. There are certain stars, known as Cepheid variables, which undergo a regular fluctuation of light of a characteristic kind, generally with a period of a few days. This light change is not due to eclipse. Moreover, the colour quality of the light changes between maximum and minimum, evidently pointing to a periodic change in the physical condition of the star. Although these objects were formerly thought to be double stars, it now seems clear that this was a misinterpretation of the spectroscopic evidence. There is, in fact, no room for the hypothetical companion star; the orbit is so small that we should have to place it inside the principal star. Everything points to the period of the light pulsation being something intrinsic in the star; and the hypothesis advocated by Shapley, that it represents a mechanical pulsation of the star, seems to be the most plausible. I have already mentioned that the observed period does, in fact, agree with the calculated period of mechanical pulsation, so that the pulsation explanation survives one fairly stringent test. But whatever the cause of the variability, whether pulsation or rotation, provided only that it is intrinsic in the star, and not forced from outside, the density must be the leading factor in determining the period. If the star is contracting so that its density changes appreciably, the period cannot remain constant. Now, on the contraction hypothesis the change of density must amount to at least 1 per cent. in forty years. (I give the figures for δ Cephei, the best-known variable of this class.) The corresponding change of period should be very easily detectable. For δ Cephei the period ought to decrease 40 seconds annually.
Now δ Cephei has been under careful observation since 1785, and it is known that the change of period, if any, must be very small. S. Chandler found a decrease of period of 1/20 second per annum, and in a recent investigation E. Hertz-sprung has found a decrease of 1/10 second per annum. The evidence that there is any decrease at all rests almost entirely on the earliest observations made before 1800, so that it is not very certain; but in any case the evolution is proceeding at not more than 1/400 of the rate required by the contraction hypothesis. There must at this stage of the evolution of the star be some other source of energy which prolongs the life of the star 400-fold. The time-scale so enlarged would suffice for practically all reasonable demands.
I hope the dilemma is plain. Either we must admit that whilst the density changes 1 per cent. a certain period intrinsic in the star can change no more than 1/800 of 1 per cent., or we must give up the contraction hypothesis.
If the contraction theory were proposed to-day as a novel hypothesis I do not think it would stand the smallest chance of acceptance. From all sides—biology, geology, physics, astronomy—it would be objected that the suggested source of energy was hopelessly inadequate to provide the heat spent during the necessary time of evolution; and, so far as it is possible to interpret observational evidence confidently, the theory would be held to be negatived definitely. Only the inertia of tradition keeps the contraction hypothesis alive—or, rather, not alive, but an unburied corpse. But if we decide to inter the corpse, let us frankly recognise the position in which we are left. A star is drawing on some vast reservoir of energy by means unknown to us. This reservoir can scarcely be other than the sub-atomic energy which, it is known, exists abundantly in all matter; we sometimes dream that man will one day learn how to release it and use it for his service. The store is well-nigh inexhaustible, if only it could be tapped. There is sufficient energy in the sun to maintain its output of heat for 15 billion years.
Certain physical investigations in the past year, which I hope we may hear about at this meeting, make it probable to my mind that some portion of this sub-atomic energy is actually being set free in the stars. F. W. Aston’s experiments seem to leave no room for doubt that all the elements are constituted out of hydrogen atoms bound together with negative electrons. The nucleus of the helium atom, for example, consists of four hydrogen atoms bound with two electrons. But Aston has further shown conclusively that the mass of the helium atom is less than the sum of the masses of the four hydrogen atoms which enter into it; and in this, at any rate, the chemists agree with him. There is a loss of mass in the synthesis amounting to about 1 part in 120, the atomic weight of hydrogen being 1.008 and that of helium just 4. I will not dwell on his beautiful proof of this, as you will no doubt, be able to hear it from himself. Now mass cannot be annihilated, and the deficit can only represent the mass of the electrical energy set free in the transmutation. We can therefore at once calculate the quantity of energy liberated when helium is made out of hydrogen. If 5 percent of a star’s mass consists initially of hydrogen atoms, which are gradually being combined to form more complex elements, the total heat liberated will more than suffice for our demands, and we need look no further for the source of a star’s energy.
But is it possible to admit that such a transmutation is occurring? It is difficult to assert, but perhaps more difficult to deny, that this is going on. Sir Ernest Rutherford has recently been breaking down the atoms of oxygen and nitrogen, driving out an isotope of helium from them; and what is possible in the Cavendish Laboratory may not be too difficult in the sun. I think that the suspicion has been generally entertained that the stars are the crucibles in which the lighter atoms which abound in the nebulæ are compounded into more complex elements. In the stars matter has its preliminary brewing to prepare the greater variety of elements which are needed for a world of life. The radio-active elements must have been formed at no very distant date; and their synthesis, unlike the generation of helium from hydrogen, is endothermic. If combinations requiring the addition of energy can occur in the stars, combinations which liberate energy ought not to be impossible.
We need not bind ourselves to the formation of helium from hydrogen as the sole reaction which supplies the energy, although it would seem that the further stages in building up the elements involve much less liberation, and sometimes even absorption, of energy. It is a question of accurate measurement of the deviations of atomic weights from integers, and up to the present hydrogen is the only element for which Dr. Aston has been able to detect the deviation. No doubt we shall learn more about the possibilities in due time. The position may be summarised in these terms: the atoms of all elements are built of hydrogen atoms bound together, and presumably have at one time been formed from hydrogen; the interior of a star seems as likely a place as any for the evolution to have occurred; whenever it did occur a great amount of energy must have been set free; in a star a vast quantity of energy is being set free which is hitherto unaccounted for. You may draw a conclusion if you like.
If, indeed, the sub-atomic energy in the stars is being freely used to maintain their great furnaces, it seems to bring a little nearer to fulfilment our dream of controlling this latent power for the well-being of the human race—or for its suicide.
So far as the immediate needs of astronomy are concerned, it is not of any great consequence whether in this suggestion we have actually laid a finger on the true source of the heat. It is sufficient if the discussion opens our eyes to the wider possibilities. We can get rid of the obsession that there is no other conceivable supply besides contraction, but we need not again cramp ourselves by adopting prematurely what is perhaps a still wilder guess. Rather we should admit that the source is not certainly known, and seek for any possible astronomical evidence which may help to define its necessary character. One piece of evidence of this kind may be worth mentioning. It seems clear that it must be the high temperature inside the stars which determines the liberation of energy, as H. N. Russell has pointed out (Pubns. Ast. Soc. Pacific, August, 1919). If so, the supply may come mainly from the hottest region at the centre. I have already stated that the general uniformity of the opacity of the stars is much more easily intelligible if it depends on scattering rather than on true absorption; but it did not seem possible to reconcile the deduced stellar opacity with the theoretical scattering coefficient. Within reasonable limits it makes no great difference in our calculations at what parts of the star the heat energy is supplied, and it was assumed that it comes more or less evenly from all parts, as would be the case on the contraction theory. The possibility was scarcely contemplated that the energy is supplied entirely in a restricted region round the centre. Now, the more concentrated the supply, the lower is the opacity requisite to account for the observed radiation. I have not made any detailed calculations, but it seems possible that for a sufficiently concentrated source the deduced and the theoretical coefficients could be made to agree, and there does not seem to be any other way of accomplishing this. Conversely, we might perhaps argue that the present discrepancy of the coefficients shows that the energy supply is not spread out in the way required by the contraction hypothesis, but belongs to some new source available only at the hottest, central part of the star.
I should not be surprised if it is whispered that this address has at times verged on being a little bit speculative; perhaps some outspoken friend may bluntly say that it has been highly speculative from beginning to end. I wonder what is the touchstone by which we may test the legitimate development of scientific theory and reject the idly speculative. We all know of theories which the scientific mind instinctively rejects as fruitless guesses; but it is difficult to specify their exact defect or to supply a rule which will show us when we ourselves do err. It is often supposed that to speculate and to make hypotheses are the same thing; but more often they are opposed. It is when we let our thoughts stray outside venerable, but sometimes insecure, hypotheses that we are said to speculate. Hypothesis limits speculation. Moreover, distrust of speculation often serves as a cover for loose thinking; wild ideas take anchorage in our minds and influence our outlook; whilst it is considered too speculative to subject them to the scientific scrutiny which would exorcise them.
If we are not content with the dull accumulation of experimental facts, if we make any deductions or generalisations, if we seek for any theory to guide us, some degree of speculation cannot be avoided. Some will prefer to take the interpretation which seems to be indicated most immediately and at once adopt that as an hypothesis; others will rather seek to explore and classify the widest possibilities which are not definitely inconsistent with the facts. Either choice has it dangers: the first may be too narrow a view and lead progress into a cul-de-sac; the second may be so broad that it is useless as a guide, and diverges indefinitely from experimental knowledge. When this last case happens, it must be concluded that the knowledge is not yet ripe for theoretical treatment and that speculation is premature. The time when speculative theory and observational research may profitably go hand in hand is when the possibilities, or at any rate the probabilities, can be narrowed down by experiment, and the theory can indicate the tests by which the remaining wrong paths may be blocked up one by one.
The mathematical physicist is in a position of peculiar difficulty. He may work out the behavior of an ideal model of material with specifically defined properties, obeying mathematically exact laws, and so far his work is unimpeachable. It is no more speculative than the binomial theorem. But when he claims a serious interest for his toy, when he suggests that his model is like something going on in Nature, he inevitably begins to speculate. Is the actual body really like the ideal model? May not other unknown conditions intervene? He cannot be sure, but he cannot suppress the comparison; for it is by looking continually to Nature that he is guided in his choice of a subject. A common fault, to which he must often plead guilty, is to use for the comparison data over which the more experienced observer shakes his head; they are too insecure to build extensively upon. Yet even in this, theory may help observation by showing the kind of data which it is especially important to improve.
I think that the more idle kinds of speculation will be avoided if the investigation is conducted from the right point of view. When the properties of an ideal model have been worked out by rigorous mathematics, all the underlying assumptions being clearly understood, then it becomes possible to say that such-and-such properties and laws lead precisely to such-and-such effects. If any other disregarded factors are present, they should now betray themselves when a comparison is made with Nature. There is no need for disappointment at the failure of the model to give perfect agreement with observation; it has served its purpose, for it has distinguished what are the features of the actual phenomena which require new conditions for their explanation. A general preliminary agreement with observation is necessary, otherwise the model is hopeless; not that it is necessarily wrong so far as it goes, but it has evidently put the less essential properties foremost. We have been pulling at the wrong end of the tangle, which has to be unravelled by a different approach. But after a general agreement with observation is established, and the tangle begins to loosen, we should always make ready for the next knot. I suppose that the applied mathematician whose theory has just passed one still more stringent test by observation ought not to feel satisfaction, but rather disappointment—"Foiled again! This time I had hoped to find a discordance which would throw light on the points where my model could be improved." Perhaps that is a counsel of perfection; I own that I have never felt very keenly a disappointment of this kind.
Our model of Nature should not be like a building—a handsome structure for the populace to admire, until in the course of time someone takes away a corner-stone and the edifice comes toppling down. It should be like an engine with movable parts. We need not fix the position of any one lever; that is to be adjusted from time to time as the latest observations indicate. The aim of the theorist is to know the train of wheels which the lever sets in motion—that binding of the parts which is the soul of the engine.
In ancient days two aviators procured to themselves wings. Dædalus flew safely through the middle air across the sea, and was duly honoured on his landing. Young Icarus soared upwards towards the sun until the wax which bound his wings melted, and his flight ended in fiasco. In weighing their achievements perhaps there is something to be said for Icarus. The classic authorities tell us that he was only "doing a stunt," but I prefer to think of him as the man who certainly brought to light a constructional defect in the flying-machines of his day. So, too, in science. Cautious Dædalus will apply his theories where he feels most confident they will safely go; but by his excess of caution their hidden weaknesses cannot be brought to light. Icarus will strain his theories to the breaking-point until the weak joints gape. For a spectacular stunt? Perhaps partly; he is often very human. But if he is not yet destined to reach the sun and solve for all time the riddle of its constitution, yet he may hope to learn from his journey some hints to build a better machine.
1. H. N. Russell, Publications of the Astronomical Society of the Pacific 31, 205 (1919).
2. A. S. Eddington, Observatory 42, 371 (1919).
3. J. H. Jeans, Nature 70, 101 (1904).
4. T. C. Chamberlin, Science 9, 889, 10, 11 (1899), and Annual Report of the Smithsonian Institution for 1899 (1900), p. 223.
1. E.g. for iron non-ionised the theoretical scattering is 5.2, against an astronomical value 120. If 16 electrons (2 rings) are broken off, the theoretical coefficient is 0.9, against an astronomical value 35. For different assumptions as to ionisation the values chase one another, but cannot be brought within reasonable range.
2. As an illustration of these limits, iron has 26 outer electrons; if 10 break away the average molecular weight is 5; if 18 break away the molecular weight is 3. Eggert (Phys. Zeits., 20, 570 [1919]) has suggested by thermodynamical
reasoning that in most cases the two outer rings (16 electrons) would break away in the stars. The comparison of theory and observation for the dwarf stars also points to a molecular weight a little greater than 3.
3. By admitting plausible assumptions closer limits could be drawn. Taking the molecular weight as 3.5, and assuming that the most critical condition is when 1/3 of gravitation is counterbalanced (by analogy with the case of rotating spheroids, in which centrifugal force opposes gravitation and creates instability), we find that the critical mass is just twice that of the sun, and stellar masses may be expected to cluster closely round this value.
4. I have taken the ratio of specific heats at the extreme possible value, 5/3; that is to say, no allowance has been made for the energy needed for ionisation and internal vibrations of the atoms, which makes a further call on the scanty supply available.