Physics
Fluid Pressure
Chapter II Why the Weight of Liquids is in Proportion To Their Height.
We see by all these examples that a small filament of water may keep a great weight in equilibrium: it remains to show what is the reason for this increase of force; we proceed to do this by the following experiment (Fig. 25):
If a vessel full of water, otherwise completely closed, has two openings, one of which is one hundred times as large as the other; by putting in each of these a piston which fits it exactly, a man pushing on the small piston will exert a force equal to that of one hundred men who are pushing on the piston which is one hundred times as large, and will overcome the force of ninety nine men.
Whatever proportion there is between these openings, if the forces which are applied to the pistons are proportional to the openings, they will be in equilibrium. Hence it appears that a vessel full of water is a new principle of mechanics, and a new machine to multiply forces to any degree we please, since a man in this way can lift any load that is given to him.
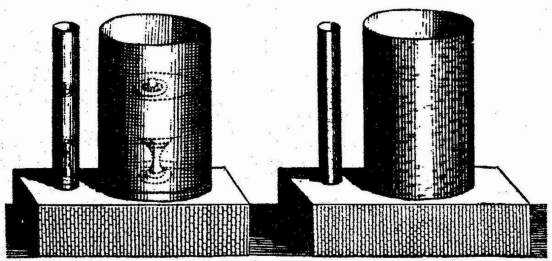 FIG. 25.
FIG. 25.
And it is truly admirable that there is encountered in this new machine the constant rule which appears in all the older machines, such as the lever, the wheel and axle, the endless screw, etc., which is, that the path is increased in the same proportion as the force; for it is clear that, since one of these openings is one hundred times as large as the other, if the man who pushes on the small piston moves it forward an inch, he will push out the other one only one one-hundredth part of an inch, for, since this movement occurs because of the continuity of the water which acts between the pistons, so that the one of them cannot move without moving the other, it is evident that, when the small piston is moved through an inch of water, which has been pushed forward by it, and which pushes the other piston, since the opening through which it moves is one hundred times as large, it will occupy only one one-hundredth of the height. So that the path is to the path as the force to the force; and this rule we may consider as the true cause of this effect: it is clear that it is the same thing to make one hundred pounds of water move one inch as to make one pound of water move one hundred inches; and thus when a pound of water is so situated in relation to one hundred pounds of water that the one hundred pounds cannot move an inch without making the pound move one hundred inches, they must remain in equilibrium, a pound having as much force to make one hundred pounds move an inch as one hundred pounds have to make a pound move one hundred inches.
It may be added, for greater clearness, that the water is under equal pressure under the two pistons; for if one of them has one hundred times more weight than the other it also touches one hundred times as many parts of the liquid, and so each part is equally pressed; therefore all parts ought to be at rest, because there is no reason why one should yield rather than the other. So that if a vessel has only a single opening, an inch across for example, in which there is a piston loaded with a pound weight, this weight presses against all parts of the vessel generally, because of the continuity and the fluidity of the water: but to determine the pressure of each part we have the following rule: Each part an inch large, like the opening, is subjected to as much pressure as if it were pushed by a pound weight (without counting the weight of the water, of which I do not here speak, for I am speaking only of the weight of the piston), because the weight of a pound presses the piston which is in the opening, and each portion of the vessel more or less great is subjected to pressure precisely more or less in proportion to its size, whether this portion is opposite the opening or at the side, far or near; for the continuity and the fluidity of the water make all these things equal and indifferent; so that it is necessary that the material of which the vessel is made should have sufficient resistance in all its parts to sustain all these forces; if the resistance is less in any one of these places, it yields; if it is greater, it provides all the necessary force and the rest remains useless in the circumstances; so that if a new opening is made in the vessel there would be needed to check the water which would gush out, a force equal to the resistance which this part ought to present, that is to say, a force which should be to the force of a pound as this last opening is to the first.
Chapter III Examples and Reasons for the Equilibrium
If a vessel full of water has two openings, to each one of which is fastened a vertical tube; if water is poured into the one and into the other to the same height, the columns of water will be in equilibrium. (Fig. 25.)
For since their heights are equal, they will be in proportion to their magnitudes, that is to say, to their openings, therefore the two masses of water in these tubes are properly two pistons whose weights are proportional to their openings; therefore they will be in equilibrium, by the preceding demonstration.
Hence it follows that, if we pour water into one of these tubes only, it will make the water rise in the other one until it has come to the same height, and then the water will remain in equilibrium, for then the water columns will be two pistons, the weights of which are in proportion to their openings.
This is the reason why water rises as high as its source.
If different liquids are placed in the tubes, such as water in the one and quicksilver in the other, these two liquids will be in equilibrium when their heights are inversely proportional to their weights; that is to say, when the height of the water is fourteen times as great as the height of the quicksilver, because quicksilver weighs fourteen times as much as water does; for then there will be two pistons, one of water and one of quicksilver, of which the weights are proportional to the openings.
And even when the tube full of water is one hundred times narrower than that in which the quicksilver is, this little thread of water will hold in equilibrium all the great mass of quicksilver, provided that it is fourteen times as high.
All that we have said up to this point about tubes can be applied to any vessel whatever, regular or not; for the same equilibrium occurs in any case: so that, if, in place of these two tubes that we have represented at the two openings, there are two vessels used; which are applied also to these openings but which are large in some places, narrow in others, and indeed entirely irregular in all their extent; when liquids have been poured in to the heights which we have described, these liquids will also be in equilibrium in these irregular tubes, just as they were in the uniform tubes, because the weight of liquids is measured only by their heights and not by their sizes.
Chapter V On Bodies Which Are Immersed in Water
We see by the former chapter that water pushes upward those bodies which it touches from below; that it pushes downward those bodies which it touches from above; and that it pushes toward one side those which it touches on the opposite side: from which it is easy to conclude that when a body is entirely immersed in water, since the water touches it above, below and on all its sides, it strives to push the body upward, downward and in every direction: but since its height is the measure of its force in all these actions, it is easy to see which of all these forces ought to prevail
For it appears, first, that since it has the same height of water on all the faces of its sides, they will be pushed equally; and therefore the body will not be moved sideways in any direction, any more than a weather-vane between two equal winds. But since the water has more height on the lower face than on the upper face, it is clear that it will push the body more upward than downward: since the difference of these heights of the water is the height of the body itself, it is easy to understand that the water pushes it more upward than downward with a force equal to the weight of the volume of water equal to that of the body.
So that a body which is in water is borne up, in the same way as if it were in one scale of a balance, and the other were loaded with a volume of water equal to its own, from which it appears that a body of copper or of any other matter which weighs more than an equal volume of water, will sink; for its weight exceeds that which counterbalances it.
If a body is of wood, or of some other matter lighter than an equal volume of water, it rises with the force by which the weight of the water is greater than its weight.
And if it is of equal weight, it neither sinks nor rises; as wax does, which stays almost in the same place in water when it is once put there.