The Cosmical Constants

Paul Adrien Maurice Dirac

(Nature 139, 323 [1937])

THE FUNDAMENTAL CONSTANTS of physics, such as c the velocity of light, h Planck’s constant, e the charge and m mass of the electron, and so on, provide for us a set of absolute units for measurement of distance, time, mass, etc. There are, however, more of these constants than are necessary for this purpose, with the result that certain dimensionless numbers can be constructed from them. The significance of these numbers has excited much interest in recent times, and Eddington has set up a theory for calculating each of them purely deductively. Eddington’s arguments are not always rigorous, and, while they give one the feeling that they are probably substantially correct in the case of the smaller numbers (the reciprocal fine-structure constant hc/e² and the ratio of the mass of the proton to that of the electron), the larger numbers, namely the ratio of the electric to the gravitational force between electron and proton, which is about 10³⁹. and the ratio of the mass of the universe to the mass of the proton, which is about 10⁷⁸, are so enormous as to make one think that some entirely different type of explanation is needed for them.

According to current cosmological theories, the universe had a beginning about

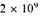
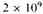
years ago, when all the spiral nebulae were shot out from a small region of space, or perhaps from a point. If we express this time, years, in units provided by the atomic constants, say the unit e²/mc³, we obtain a number about 10³⁹. This suggests that the above-mentioned large numbers are to be regarded, not as constants, but as simple functions of our present epoch, expressed in atomic units. We may take it as a general principle that all large numbers of the order 10³⁹, 10⁷⁸ ... turning up in general physical theory are, apart from simple numerical coefficients, just equal to t, t² ..., where t is the present epoch expressed in atomic units. The simple numerical coefficients occurring here should be determinable theoretically when we have a comprehensive theory of cosmology and atomicity. In this way we avoid the need of a theory to determine numbers of the order 10³⁹.

Let us examine some of the elementary consequences of our general principle. In the first place, we see that the number of protons and neutrons in the universe must be increasing proportionally to t². Present-day physics, both theoretically and experimentally, provides no evidence in favour of such an increase, but is much too imperfect to be able to assert that such an increase cannot occur, as it is so small; so there is no need to condemn our theory on this account. Whether the increase is a general property of matter or occurs only in the interior of stars is a subject for future speculation.

A second consequence of our principle is that, if we adopt a scheme of units determined by atomic constants, the gravitational ’constant’ must decrease with time, proportionally to t^-1. Let us define the gravitational power of a piece of matter to be its mass multiplied by the gravitational constant. We then have that the gravitational power of the universe, and presumably of each spiral nebula, is increasing proportionally to t. This is to some extent equivalent to Milne’s cosmology¹, in which the mass remains constant and the gravitational constant increases proportionally to t. Following Milne, we may introduce a new time variable,

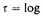t, and arrange for the laws of mechanics to take their usual form referred to this new time.

To understand the present theory from the point of view of general relativity, we must suppose the element of distance defined by

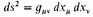
in the Riemannian geometry to be, not the same as the element of distance in terms of atomic units, but to differ from this by a certain factor. (The former corresponds to Milne’s dτ and the latter to Milne’s dt.) This factor must be a scalar function of position, and its gradient must determine the direction of average motion of the matter at any point.

1. Dirac modified and enlarged upon this contribution in his article in the Proceedings of the Royal Society (London) A165, 199 (1938).

2. A. S. Eddington, Monthly Notices of the Royal Astronomical Society 92, 3 (1932). Proceedings of the Cambridge Philosophical Society 40, 37 (1944). See also Eddington’s Fundamental Theory, ed. E. T. Whittaker (Cambridge: Cambridge University Press, 1948).

3. At nearly the same time S. Sambursky (Physical Review 52, 335 [1937]) independently showed that the observed redshifts of nebulae are consistent with a static, nonexpanding universe when one assumes that the radius of the electron and the other universal lengths of atomic physics decrease with time. Instead of postulating a growing world radius, Sambursky reasoned that the so-called quantum of action, h(Planck’s constant), and also G decrease with time.

4. C. Brans and R. H. Dicke, Physical Review 124, 925 (1961); F. Hoyle and J. V. Narlikar, Monthly Notices of the Royal Astronomical Society 155, 323 (1972); P. A. M. Dirac, Proceedings of the Royal Society (London) A333, 403 (1973).

5. A. M. Wolfe, R. L. Brown, and M. S. Roberts, Physical Review Letters 37, 179 (1976).

1. Milne, Proc. Roy. Soc. A158, 324 (1937).