Infinite Series

Nicole Oresme

Translated and annotated by Edward Grant¹

QUESTION 1

Concerning the book of Euclid [that is, the

Elements], we inquire first about a certain statement by Campanus asserting that a magnitude decreases into infinity.² First we inquire whether a magnitude decreases into infinity according to proportional parts.

In the first place, it is argued that it does not [increase into infinity according to proportional parts]. In a continuum there are not infinite parts of the same [finite] quantity, therefore there are not infinite parts of the same proportion. The antecedent is obvious, for then it would be infinite;³ the consequent is clear because any proportional part is part of the same quantity with any other [proportional part]. Therefore, the parts of the same proportion and of the same quantity are the same.⁴

In the comment by Campanus the opposite [of this] is obvious.

For this question, these things must be noted: firstly, what has [already] been said, namely that proportional parts are⁵ parts of the same proportion; secondly, in how many ways can such parts be imagined; thirdly, how something can be divided into such parts; fourthly, assumptions and propositions.

As to the first, it must be noted that proportional parts are said to be in continued proportion and such a proportion is a similitude of ratios, as it is called in the comment [by Campanus] on the ninth definition of the fifth [book of Euclid],⁶ where it is said that such a [relation or similitude] is had between at least two ratios; and for this reason Euclid says that the least number of terms in which it [that is, similitude of ratios] is found is three, but he does not give a maximum number because it is a process [that continues] into infinity. It follows from this that it is not proper to speak of [a single] proportional part, nor of two proportional parts, but it is necessary that there be at least three⁷ and there can be an infinite number. Proportional parts are said to be continually proportional because the first [proportional part] is related to the second as the second to the third, and so on if more are taken.

As to the second point, I reply that a division can be made into such proportional parts in as many ways as there are continuous proportionals; and there are just as many continuous proportionals as there are ratios, namely infinitely many. For example, it can happen that the first [proportional part] is double the second, and the second double the third, and so on,⁸ just as is commonly said about the division of a continuum; and it could happen that the first [proportional part] is triple the second and the second triple the third, and so on.⁹

As to the third point, it is held that a line and any continuum can be divided into such [proportional] parts. A line [can be so divided] in two ways because there are two extremities of it and such parts can begin from either one. A surface [can be divided into proportional parts] in infinite ways, and similarly for a body.

As to the fourth point, a first supposition is assumed such that if any ratio were increased to infinity with the greater term unchanged, the smaller term would be diminished into infinity. This is obvious, since a ratio between two [terms] can be increased into infinity in two ways: either by the augmentation to infinity of the greater term or by the diminution to infinity of the lesser term.¹⁰

A second supposition is that if to any ratio there is added so much, and again so much, and so on into infinity, this ratio will be increased into infinity; and this is common to all quantities.

A third supposition is this: that to any quantity an addition can be made by proportional parts; and by the same [supposition] a diminution can be made by proportional parts.

The first proposition is that if an aliquot part should be taken from some quantity, and from the first remainder such a part is taken, and from the second remainder such a part is taken, and so on into infinity, such a quantity would be consumed exactly—no more, no less—by such a mode of subtraction,¹¹ This is proved because the whole that was originally assumed, and the first remainder, and the second remainder, and the third, and so on, are continually proportional, as could be proved when arguing with an altered ratio.¹² Therefore, there is a certain ratio, and then so much [of it], and so on endlessly; consequently, such a ratio of the whole to the remainder increases to infinity, because, by the second supposition, it is composed of these [ratios].¹³ And the other term, say the whole, is imagined as unchanged, so that, by the first supposition, the remainder is diminished into infinity, and consequently, the Whole quantity is consumed exactly.

This corollary follows: If from any foot [length] there should be taken away a half foot, and then half of the remainder of this quantity, and then half of the next remainder, and so on into infinity, the foot length will be removed exactly by this [procedure].¹⁴

A second corollary is that if one-thousandth part of a foot were taken away [or removed], then [if] one-thousandth part of the remainder of this foot [were removed], and so on into infinity, exactly one foot would be subtracted from this [original foot].¹⁵

But this is doubted. Since exactly half of one foot and then half of the remainder of that foot, and so on into infinity, make one foot, let this whole [foot] be a; similarly, by the second corollary, one-thousandth part of this one foot,and one-thousandth of another [that is, the next] remainder, and so on into infinity, make one foot, let this be b. It is then obvious that a and b are equal. But it can be proved that they are not equal because the first part of a is greater than the first part of b; and the second part of a [is greater] than the second [part] of b, and so on to infinity, Therefore, the whole a is greater than the whole b. And this is confirmed, [for] if Socrates were moved over a for one hour and Plato over b [for one hour], and [if] they divide the hour by proportional parts and traverse a and b, respectively, then Socrates is moved quicker than Plato in the first proportional part; and similarly in the second [proportional part], and so beyond. Socrates will therefore traverse a greater distance than Plato, so that a is a greater distance than b.¹⁶ In response to this, I deny the antecedent, namely that the first part of a is greater [than the first part of b, and the second part of a is greater than the second part of b], and so on. The reason [for denying the antecedent] is that although the first part of a is greater than the first part of b, and the second part of a is greater than the second part of b, this is not so into infinity, since one part will eventually be reached that will not be greater than the part of b to be compared, but smaller. In this way the response to the question is clear, because in the imagination any continuum can have infinite proportional parts; similarly, the first [part] can really be separated from the others in thought¹⁷ and then the second, and so on into infinity.

As for the argument to the contrary, I deny the consequent, and for proof I say that although any proportional part belongs to the same quantity as any other [proportional part], it is nevertheless not of the same quantity with that [part] with which it is of the same proportion. They are not equals, since it follows [that if] they are equals, therefore they are mutually equal to themselves.¹⁸

QUESTION 2

Next we inquire whether an addition to any magnitude could be made into infinity by proportional parts. . . .¹⁹

For this question, it must be noted in the first place that there is a ratio of equality and it is between equals; another [kind of ratio] is a ratio of greater inequality, which is of greater to smaller, as 4 to 2; and another [kind] is [a ratio] of lesser inequality, which is of smaller to greater, as 2 to 4. And these names differ with respect to relative superposition and subposition,²⁰ as is obvious in what has been said before; and by this there are three ways in which an addition can be made to any quantity.

Secondly, it must be noted that if an addition were made to infinity by proportional parts in a ratio of equality or of greater inequality, the whole would become infinite;²¹ if, however, this addition should be made [by proportional parts] in a ratio of lesser inequality, the whole would never become infinite, even if the addition continued into infinity.²² As will be declared afterward, the reason is because the whole will bear a certain finite ratio to the first [magnitude] assumed [or taken] to which the addition is made.

Finally, it must be noted that every term smaller than another which bears to it [that is, to the greater] a fixed ratio is called a fraction or fractions, or part or parts; and this is obvious in the principles of the seventh book of Euclid, and it is denominated by two numbers, one of which is the numerator and the other the denominator, as is clear in the same place [that is, in the principles of Euclid’s seventh book].²³ For example, one is smaller than two and is called one-half of two and one-third of three, and so on; and two is called two-thirds of three and two-fifths of five, and they ought to be written in this way;²⁴ and the two is called the numerator, the five the denominator.

The first proposition is that if a one-foot quantity should be assumed and an addition were made to it into infinity according to a subdouble [that is, one-half] proportion so that one-half of one foot is added to it, then one-fourth [of one foot], then one-eighth, and so on into infinity by squaring the halves,²⁵ the whole will be exactly double the first [magnitude] assumed.²⁶ This is obvious, because if these [very] parts were taken from any quantity, exactly double the first quantity would be taken, as is clear from the first question preceding. By a parity of reasoning, then, if the parts were added [the whole would be exactly double the first].²⁷

The second proposition is this: If any quantity were assumed, say one foot, then let one-third as much be added [to it], and then [let] one-third of what was added [be added to the sum], and so on into infinity, the whole will be exactly

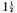
feet, namely in a sesquialterate ratio to the first quantity assumed.²⁸ Furthermore, this rule should be known: We must see how much the second part falls short of the first part, and [how much] the third [falls short] of the second, and so on with the others, and to denominate this [difference] by its denomination, and then the ratio of the whole aggregate to the quantity [first] assumed will be just as a denominator to a numerator. For example, in what was [just] proposed, the second part, which is one-third of the first, falls short by two-thirds of the [quantity of the] first, so that the ratio of the whole to the first part, or what was assumed, is as 3 to 2 and this is a sesquialterate [ratio].²⁹

The third proposition is this: It is possible that an addition could be made, though not proportionally, to any quantity by ratios of lesser inequality, and yet the whole would become infinite; but if it were done proportionally, it would be finite, as was said. For example, let a one-foot quantity be assumed to which one-half of a foot is added during the first proportional part of an hour, then one-third of a foot in another [or next proportional part of an hour], then one-fourth [of a foot], then one-fifth, and so on into infinity following the series of [natural] numbers, I say that the whole would become infinite,³⁰ which is proved as follows: There exist infinite parts of which any one will be greater than one-half foot and [therefore] the whole will be infinite. The antecedent is obvious, since 1/4 and 1/3 are greater than 1/2; similarly [the sum of the parts] from 1/5 to 1/8 [is greater than 1/2] and [also the sum of the parts] from 1/9 to 1/16, and so on into infinity. . . .³¹

^1. This selection is from Oresme’s Questions on the Geometry of Euclid, written perhaps around 1350. The translation, containing all but a few lines of the first two questions, is based upon the Latin text edited by H. L. L. Busard, Nicole Oresme: Quaestiones super geometriam Euclidis (Leiden: Brill, 1961), pp. 1–6, and the many emendations and corrections to that text made by John E. Murdoch in his long review of Busard’s text in Scripta Mathematica, XXVII (1964), 67–91.

The subject of infinite series, with its associated paradoxes, exerted a strong fascination for medieval natural philosophers and mathematicians. Many series were formulated and utilized by Oxford (Merton College) scholastics such as Swineshead, Dumbleton, Heytesbury, and others in the first half of the fourteenth century, and then by Parisian scholastics such as Nicole Oresme and, much later, Alvarus Thomas, to name only two; for some of the infinite series proposed by Alvarus Thomas, see H. Wieleitner, "Zur Geschichte der unendlichen Reihen im christlichen Mittelalter," Bibliotheca Mathematica, XIV (1914), 150—168.

^2. Immediately following the axioms (communes animi conceptiones) and just before Book I of Euclid’s Elements, Campanus of Novara remarks that "magnitude decreases into infinity, but in numbers this is not so."

^3. Presumably, a defender of this position would argue that if a continuous quantity consisted of an infinite number of parts, it would be infinite.

^4. Since there cannot be an infinite number of parts in a finite quantity, there cannot be an infinite number of proportional parts, because "the parts of the same proportion and of the same quantity are the same." In the concluding paragraph of this question, Oresme interprets this argument to mean that all proportional parts are equal, an absurd position which he promptly denies without elaboration, for it is contrary to all that has been shown in the question itself.

^5. Although the text has vel (or), the sense seems to require "are."

^6. For a translation of this definition, see Selection 27, Definition 9.

^7. If three terms, a, b, and c, are in continued proportion, then

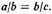
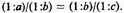
In the same way, a proportion of proportional parts must consist of at least three proportional parts in continued proportion, as, for example, Hence at least three such ratios are required before we can speak of proportional parts. Murdoch remarks (p. 68), "The key notion in his analysis is correctly seen by Oresme to be that of ’proportional parts,’ parts determined, he adds, by a given continued proportion. Thus, his fundamentals for an investigation of infinite geometric series are in fine order. Moreover, when he probes further his success is, by fourteenth-century standards, considerable."

^8. That is, (1/2)ⁿ, where

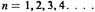
^9. That is, (1/3)ⁿ, where

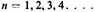
^10. Oresme does not say but this supposition can apply only to ratios of greater inequality. He makes this quite explicit in his On Ratios of Ratios (De proportionibus proportionum,) ch. 1, ll. 106–111 (Grant, Nicole Oresme: De proportionibus [Madison, Wis.: University of Wisconsin Press, 1966], pp. 144–147.

^11. Murdoch (p. 68) represents this series as:

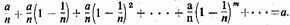
^12. By subtracting from a each successive proportional Dart in the series described in note 11, we obtain a,

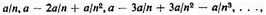
which are the successive remainders in continued proportion. These successive remainders, as Oresme tells us a few lines below, are diminished to infinity and "the whole quantity is consumed exactly."

^13. The ratio of a, the whole, to the successive remainders forms a sequence of ratios increasing to infinity. Thus the successive ratios are

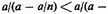
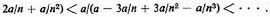
^14. Oresme expresses here the convergent series

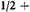
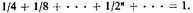
^15. Here we have the convergent series

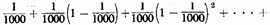
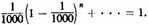
^16. This paragraph brings to the fore a doubt that arises from a comparison of corresponding terms in the series described in notes 14 and 15. Since the successive terms of the first series, called a, are greater than the corresponding terms in the second series, called b—and we see this by inspection where

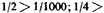
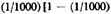
], and so on—it is concluded that the whole magnitude in series a is greater than that of series b, making it impossible for them both to sum at 1. Oresme denies this (see remainder of paragraph) by insisting rightly that eventually the terms of series b will become greater than their corresponding counterparts in series a.

^17. Although the text reads per corrupcionem, it seems to require emendation to per concepcionem, which I have translated as "in thought."

^18. See note 4.

^19. Eighteen lines, offering a few objections to the affirmative of this question, have been omitted from the translation.

^20. I have emended Busard’s text from relativi <sc. termini> posicionis to relative <super> posicionis and altered my translation accordingly. The terms 2 and 4 can be related so that one is relatively "superposed" or "subposed" to the other. Thus 4 "superposed" with respect to 2 produces a ratio of greater inequality; if "subposed"—that is, placed under 2—it produces a ratio of lesser inequality. Almost identical terminology was used by Oresme in his On Ratios of Ratios, ch. 1, ll. 201–204 (Grant, Nicole Oresme: De proportionibus, pp. 154, 155).

^21. Should the proportional parts be represented as (a/b)ⁿ, where

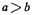
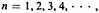
and an addition to infinity would produce an infinite whole (that is, a divergent series).

^22. Here

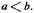
^23. In Book VII of Campanus’ edition of Euclid’s Elements, fractions are not mentioned. While Campanus speaks of denomination of ratios, he does not assert that two numbers are required to denominate a ratio nor does he identify these numbers as numerator and denominator. By "fraction or fractions, or part or parts," Oresme probably meant to distinguish between unit and non-unit fractions. That is, if a and b are numbers in their lowest terms and

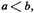
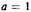
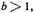
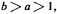
then if and we have a (unit) fraction or part; but if we have fractions or parts.

^24. Apparently Oresme intended to convey the precise manner in which fractions were to be written, but the Latin text, and presumably the manuscripts used to establish that text, fail to reveal this. It seemed best to verbalize them in full. The form desired by Oresme for expressing simple fractions is preserved in Part 1 of his Algorismus proportionum, as the reader can see in Selection 28. But just as the manuscripts of the Questions on the Geometry of Euclid display no unanimity, so also do the many manuscripts of the Algorismus present a bewildering variety of forms for representing irrational ratios.

^25. "Squaring the halves" translates duplando subduplos.

^26. That is,

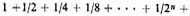
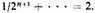
^27. If from any magnitude parts were taken in the order

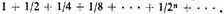
the total magnitude taken would be double the first given quantity (one foot in this case). Reversing the process and reconstituting the whole by adding the successive parts, a quantity double (that is, two feet) the first given quantity (that is, one foot) would be produced.

^28. We have here the convergent series

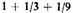
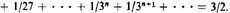
^29. The difference between the first and second terms is

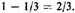
"To denominate this [difference] by its denomination" is, in medieval mathematics, to represent the quantity two-thirds by a ratio of numbers, namely 2/3. Then, when 2/3 is related as denominator to numerator, we get 3/2, the sum of the series. From the fact that Oresme offered only this example, it would appear that he intended that it apply to any two successive terms in the series. But if the second and third parts—or any other two successive parts—are taken, the concept of "denomination" cannot have its usual meaning for Oresme. 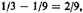For where the difference, two-ninths, is a ratio whose numerical denomination is 2/9, and the ratio of its denominator to its numerator, representing the final step, is 9/2, a result Oresme could not have intended. 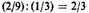Obviously, is required where the reciprocal yields 3/2. But "to denominate a difference by its denomination" cannot mean representing 2/9, the difference, by the ratio (2/9): (1/3) unless, perhaps, Oresme extended the meaning of denomination to include the case where the greater of two ratios (in this instance 1/3) can serve as the denominator and denomination of the difference (that is, 2/9). Nevertheless, one is left with the strong impression that Oresme used the expression "to denominate this [difference] by its denomination" correctly in the only instance he gives and improperly assumed that it applied equally to all instances.

^30. The series

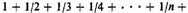
is divergent and is offered as illustration of the case in which ratios of lesser inequality are not added proportionally and can constitute an infinitely large whole.

^31. Omitted here are the remaining twenty lines of Question 2, in which Oresme replies to the objections mentioned in note 19.