First Attempt at a Theory of the Arrangement and Motion of the Sidereal System
Jacobus Cornelius Kapteyn
(Astrophysical Journal 55, 302–327 [1922])
Abstract—First attempt at a general theory of the distribution of masses, forces, and velocities in the stellar system.—(1) Distribution of stars. Observations are fairly well represented, at least up to galactic lat. 70°, if we assume that the equidensity surfaces are similar ellipsoids of revolution, with axial ratio 5.1, and this enables us to compute quite readily (2) the gravitational acceleration at various points due to such a system, by summing up the effects of each of ten ellipsoidal shells, in terms of the acceleration due to the average star at a distance of a parsec. The total number of stars is taken as
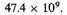
(3) Random and rotational velocities. The nature of the equidensity surfaces is such that the stellar system cannot be in a steady state unless there is a general rotational motion around the galactic polar axis, in addition to a random motion analogous to the thermal agitation of a gas. In the neighborhood of the axis, however, there is no rotation, and the behavior is assumed to be like that of a gas at uniform temperature, but with a gravitational acceleration (Gη) decreasing with the distance ρ. Therefore the density Δ is assumed to obey the barometric law:
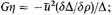
and taking the mean random velocity
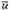
as 10.3 km/sec., the author finds that (4) the mean mass of the stars decreases from 2.2
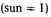
for shell II to 1.4 for shell X (the outer shell), the average being close to 1.6, which is the value independently found for the average mass of both components of visual binaries. In the galactic plane the resultant acceleration—gravitational minus centrifugal—is again put equal to
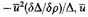
is taken to be constant and the average mass is assumed to decrease from shell to shell as in the direction of the pole. The angular velocities then come out such as to make the linear rotational velocities about constant and equal to 19.5 km/sec. beyond the third shell. If now we suppose that part of the stars are rotating one way and part the other, the relative velocity being 39 km/sec., we have a quantitative explanation of the phenomenon of star-streaming, where the relative velocity is also in the plane of the Milky Way and about 40 km/sec. It is incidentally suggested that when the theory is perfected it may be possible to determine the amount of dark matter from its gravitational effect. (5) The chief defects of the theory are: That the equidensity surfaces assumed do not agree with the actual surfaces, which tend to become spherical for the shorter distances; that the position of the center of the system is not the sun, as assumed, but is probably located at a point some 650 parsecs away in the direction galactic long. 77°, lat. -3°; that the average mass of the stars was assumed to be the same in all shells in deriving the formula for the variation of Gη with ρ on the basis of which the variation of average mass from shell to shell and the constancy of the rotational velocity were derived—hence either the assumption or the conclusions are wrong; and that no distinction has been made between stars of different types.
1. EQUIDENSITY SURFACES SUPPOSED TO BE SIMILAR ELLIPSOIDS
IN MOUNT WILSON CONTRIBUTION No. 1881 a provisional derivation was given of the star-density in the stellar system. The question was there raised whether the inflection appearing near the pole in the equidensity surfaces for small densities is real or not. I have since found that these inflections can be avoided without doing very serious violence to the results of observation. If this is done, the equidensity surfaces become approximately ellipsoids, and not only that, but the data can be represented without exceeding the possible limits of observation error, by assuming the equidensity surfaces to be concentric, similar revolution ellipsoids, similarly situated.
2. ELEMENTS OF THE ELLIPSOIDS
Taking as unit of star-density that in the neighborhood of the sun, the adopted axes of the ellipsoids, which will be referred to as ellipsoids I, II, ..., X and which correspond to the values (Δ being the density)
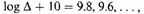
are as shown in table 80.1. The
A-axis is directed toward the galactic Pole, the
B-axis lies in the plane of the Milky Way.
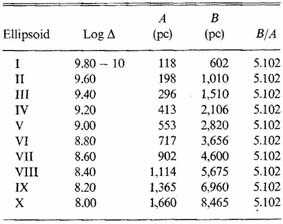Table 80.1 Equidensity ellipsoids
For the Milky Way and for the direction toward the Pole this table yields densities which are fairly well represented, for
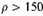
parsecs, by the formulae,
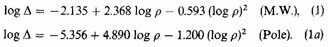
A section of the equidensity-ellipsoids through the sun (which has been assumed to be the center of the system) at right angles to the plane of the Milky Way is shown in figure 80.1.
The agreement of the densities furnished by table 80.1 with those of Contribution No. 188 is fairly good for all galactic
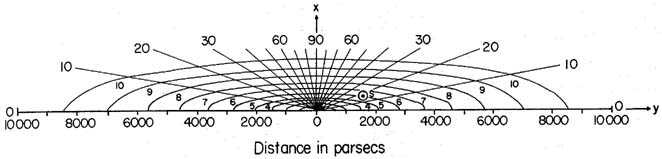Fig. 80.1 Density distribution of the stars in a plane perpendicular to the plane of our galaxy. The curves are lines of equal density, with the star density near the sun taken to be unity. The sun, S, has been assumed to be near the center of the system, and the curves marked 1, 2, 3, ..., 10 denote, respectively, relative star densities of 0.63, 0.40, 0.25, 0.19, 0.10, 0.063, 0.040, 0.025, 0.016, and 0.010.
latitudes up to 65° or 70°. For still higher latitudes it may perhaps still be called tolerable. At least the deviations hardly exceed what would be produced by an error of 0.1 mag. in the photometric scale for these regions.
In the present paper I have substituted these ellipsoids for the surfaces derived directly from observation in Contribution No. 188, not because I think they are nearer the truth, but simply because they are so enormously more convenient for further computation.
My aim in the present paper is simply to get hold of some approximate information about the real structure and motion of the system, and quantitative accuracy has been considered of secondary importance as long as we may hope that the main features are not affected. I trust that this hope will not be disappointed, notwithstanding the many defects—defects that will be duly pointed out—which still attach to the present treatment.
3. ADVANTAGE OF THE ADOPTION OF THE ELLIPSOIDS
The form of the equidensity surfaces thus adopted has the advantage that it calls attention to the possibility of determining with some precision the gravitational attraction of the whole of the stellar system on any point inside ellipsoid X, while at the same time it renders the computation of that attraction a relatively easy matter.
In another paper2 van Rhijn and I have tried to show that, as soon as we possess good counts of stars for each interval of magnitude down to apparent magnitude 17 (visual), we shall know with some tolerable approximation the density of the whole region covered by figure 80.1, that is, of the whole extent of the stellar system for which the density exceeds one-hundredth of that in the neighborhood of the sun.
In the near future such counts will be available. They will be furnished by the Mount Wilson "Catalogue of the Selected Areas" (from
to
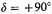
), the discussion of which is in the hands of Seares. A few provisional counts make it probable that this work will in the main confirm the elements used for table 80.1 and figure 80.1. I will assume, therefore, that even now the densities are sufficiently well known for the whole of ellipsoid X.
The advantage just alluded to is a consequence of the well-known property that the attraction of an ellipsoidal shell of constant density, bounded by two similar and similarly situated ellipsoids, on an internal point is zero. For it is evident by this property that, if in all that part of the system which lies outside ellipsoid X—for which part accurate data are still wanting—the arrangement in similar ellipsoids also holds, the attraction of this outside domain on a point inside ellipsoid X would be zero. And as the distribution of density inside ellipsoid X is known, the possibility of computing the attraction of the total system on a point inside of X becomes evident. If on the contrary the same arrangement does not hold outside ellipsoid X, it still seems highly probable a priori that any change in the form of the equidensity surfaces must be gradual, that is, the equidensity surfaces in the neighborhood of X will diverge little from similar ellipsoids, and the greater changes will begin to appear only at more considerable distances. For the consecutive shells, therefore, the attraction on an internal point will begin by being very small, both on account of the near approach to similarity of these shells and their small density and greater distance from the attracted point. For more distant shells the first circumstance will probably diminish in importance with increasing distance, while, on the contrary, the second becomes more and more important. On the whole, therefore, the attraction of all of that part of the system which lies outside X will be small, and its neglect will presumably not prevent us from obtaining fairly exact ideas about the total forces.
4. COMPUTATION OF THE GRAVITATIONAL FORCES
In ellipsoid I, which for brevity I will call shell 1, and in each of the shells 2, 3,..., 10, between the surfaces of ellipsoids I, II,..., X, the density varies between limiting values which are in the ratio of 1 to 1.585. In what follows I will assume for each shell a constant average density.
We include here only the ten points at a galactic latitude of 90° lying in surfaces of ellipsoids I, II, ... X.
As a unit of attraction I have used the attraction on each other of two stars of average mass separated by a distance of 1 parsec.
I first computed the attraction of the full ellipsoids I, II,..., X on the points specified above, on the supposition that they are of a constant density such that every cubic parsec contains a single star. The formulae for this computation are given in the Appendix.
The attraction of the full ellipsoids having been found, simple subtraction gives the attraction of the separate shells 1, 2, ..., 10, all supposed to have the density corresponding to one star per cubic parsec. The actual attraction of the shells was obtained by multiplying these results by the number of stars per cubic parsec contained in each shell. For the average densities, expressed in terms of the density in the neighborhood of the sun, I adopted the values corresponding to the logarithms 9.9, 9.7, 9.5,..., 8.1, each minus 10, multiplied by 0.0451, which according to Contribution No. 188 (12) is the number of stars per cubic parsec near the sun; this gives the numbers in table 80.2.
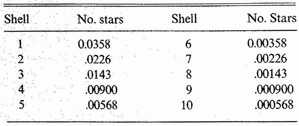Table 80.2 Average number of stars per cubic parsec
Having found the separate attractions, the components of the total attractions parallel to the axes can at once be determined by noting that the attraction of any shell on an internal point is zero, and further, by neglecting the attraction of that part of the system outside of ellipsoid X on a point inside this ellipsoid. Instead of the components I have entered in table 80.3 the total forces G and the angles that these forces make with the X-axis.
We include in table 80.3 only the forces in the direction perpendicular to the galactic plane. In this table the attraction of the whole stellar system on a body in the point I is shown to be equivalent to the attraction of 40.06 stars of average mass at a distance of 1 pc from the same body.
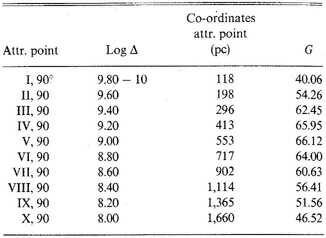Table 80.3 Total attractions of the whole system
5. ANALYTICAL REPRESENTATION OF G FOR GALACTIC LATITUDES 0° AND 90°
In trying to represent the force G by an analytical formula, I started from the consideration that, as the density is constant near the center, the attraction must be nearly proportional to the distance ρ for very small values of ρ; further, that for distances very great as compared with the dimensions of the stellar system, the attraction must be practically the same as it would be were the mass of the whole system concentrated in the center. For these latter distances, therefore, G must be proportional to
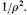
The following easily managed formula satisfies both conditions:
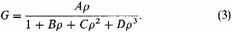
In this formula A/D evidently equals the total number of stars, N, in the stellar system.
Here Kapteyn uses data from Groningen Publication no. 27 to show that
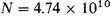
stars; using the values of
G given in table 80.3, he obtains
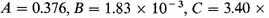
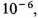
and
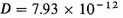
for a galactic latitude of 90°.
6. APPLICATION OF KINETIC THEORY OF GASES
The results thus far obtained rest, it is true, on provisional data, which even now might be materially improved; they further depend on the supposition, not yet fully demonstrated, that, within the distances here considered, there is no appreciable extinction of light in space, but they are, nevertheless, I think, the legitimate outcome of our data.
For what follows I will now introduce some considerations borrowed from the kinetic theory of gases, the applicability of which to the stellar system might be considered doubtful. At all events I do not pretend to have demonstrated this applicability. The results which will be derived cannot lay claim to be demonstrably correct, but they seem to me to be so remarkable that, after a good deal of hesitation, I have resolved to publish them, in the hope that others, better versed in these matters, may furnish us with a more rigorous solution of the problem involved.
Even though it has been shown, in the main by unpublished investigations, that the peculiar motions3 of the stars with some crude approximation are Maxwellian, the stellar system cannot be treated as a gas at rest; first, because of the existence of stream-motion; second, because of the form of the equidensity surfaces, which is certainly different from that of the equipotential surfaces of the gravitational force.
That they are different is proved by the fact, among others, that in general the forces are not normal to these surfaces. This is evident enough without further explanation. Moreover, it is clearly brought out by table 80.3, where the angle with the normal reaches values of more than 27°. Further it is well known that in a gas at rest under its own attraction, the equidensity surfaces are spherical.
In table 80.3 we omitted values of the density Δ and the total forces G at latitudes of 0, 30 and 57.1 degrees. Although the values of Δ decrease systematically from the inner to the outer ellipsoids at each latitude, the values of G at first increase and then decrease. This behavior is illustrated in the data given in table 80.3 for a latitude of 90 degrees.
The system cannot therefore be in a steady state unless it has a systematic motion. Since the discovery of the star-streams it is clear that such a motion really exists and that it is parallel to the plane of the Milky Way.
It seems rational, therefore, to assume that the system has a sort of rotational motion round the X-axis (see figure 80.1) which is directed toward the pole of the galaxy. The form of the equidensity surfaces found directly in Contribution No. 188 as well as that now adopted, strongly indicates some such motion.
This being assumed, the stars along the axis will still have no other motion than their peculiar motions, which, as was just mentioned, are Maxwellian, at least with some approximation. I venture to assume, therefore, that the stars in the immediate neighborhood of this axis are arranged as the molecules of a gas in a quiescent atmosphere.
If:
Δ be the star-density (number of stars per cubic parsec);
u one of the components of the peculiar velocity;
η the acceleration produced by the attraction of a star of average mass at a distance of one parsec, then on the above assumption
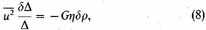
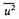
being the average value of
u2.
The formula is analogous to that used for barometric determinations of altitude in an atmosphere of constant temperature throughout. On the other hand, we have found empirically formulae such as (1) and (1a) (see also Contribution No. 188, p. 13 [21]); in other words,
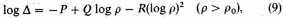
from which, by differentiation
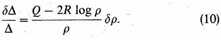
Comparing the two expressions, (8) and (10), for
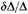
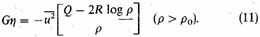
As the motions are supposed to be Maxwellian, the wellknown formula used in the theory of least squares gives
From observations of the radial velocities at the Lick Observatory, where no choice has been made on the basis of motion (Lick Observatory Bulletin 6, 126), I derived the value4
or since
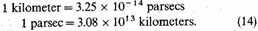
I find, in the units parsec and second, here adopted,
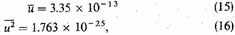
so that (11) becomes
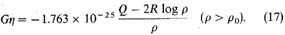
Finally, for galactic latitude 90°, we obtain from equation (1a) the values:
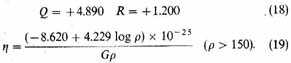
For small values of ρ, formula (9) does not hold. According to Contribution No. 188, and particularly according to Contribution No. 229, it represents the observations excellently for values of ρ well beyond the maximum (which in the present case lies near
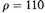
parsecs). For values of
ρ below the maximum the density is nearly constant. The differential-quotient
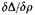
thus becomes very small and
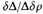
very unreliable. In the present case it will probably be well not to rely on the formula below, say, 150 parsecs. This limit was adopted in (19).
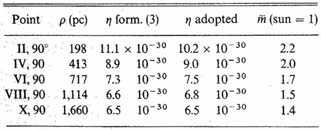
I have computed the values of η from (19) both on the supposition that G has the values found directly in table 80.3 and that it has the values yielded by formula (3). The former were adopted (table 80.4).
Table 80.4 Values of η and [figure table]
|
The quantity η is, as stated above, the acceleration per second, in parsecs, produced by the attraction of a star of average mass on a body at a distance of one parsec. The acceleration which the sun would produce, expressed in the same units, is
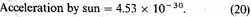
This enables us to find the average mass
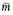
of a star expressed in the mass of the sun as a unit. The values of
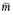
thus found have been inserted in the last column of table 80.4.
These values agree surprisingly well with what has been found by totally different considerations. In a recent paper5 Jackson and Furner find for visual binary stars, as the best average
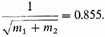
Consequently
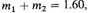
which agrees with table 80.4 if we suppose that the combined mass of the two components and not that of a single component is comparable with the mass of a single star, and especially if we further consider that there are theoretical grounds for expecting that the average mass will decrease for increasing distance.
6
REMARK: DARK MATTER
It is important to note that what has here been determined is the total mass within a definite volume, divided by the number of luminous stars. I will call this mass the average effective mass of the stars. It has been possible to include the luminous stars completely owing to the assumption that at present we know the luminosity-curve over so large a part of its course that further extrapolation seems allowable.
Now suppose that in a volume of space containing l luminous stars there be dark matter with an aggregate mass equal to Kl average luminous stars; then, evidently the effective mass equals
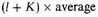
mass of a luminous star.
We therefore have the means of estimating the mass of dark matter in the universe. As matters stand at present it appears at once that this mass cannot be excessive. If it were otherwise, the average mass as derived from binary stars would have been very much lower than what has been found for the effective mass.
7. ANGULAR VELOCITIES (ω) IN THE PLANE OF THE GALAXY
Ignoring for an instant the fact that the stars in the Milky Way cannot be systematically at rest and treating the stars near this plane in the same way as those near the axis, I am led by a formula analogous to (17) to values of η which are not quite half those given in table 80.4. I suppose that the difference must be wholly due to the centrifugal force induced by the rotational motions. In fact, I assume that the average mass is the same throughout the whole system, at least for points on the same equidensity surface.
8. ANGULAR VELOCITY FOR STARS NOT IN THE GALAXY
Omitted here are Kapteyn’s computations of the forces caused by rotation about an axis centered at the sun and perpendicular to the galactic plane; also omitted are tables giving estimates for the rotational velocity at different distances from the sun in different directions.
9. EXPLANATION OF STAR-STREAMING
The most striking feature brought out by these numbers is undoubtedly the fact that at distances from the axis exceeding 2,000 parsecs the linear velocity of the stars is nearly constant, the average being 19.5 km/sec.; that is, the great bulk of the stars must have a motion of 19.5 km in a direction parallel to the plane of the Milky Way. Observation has already proved that there really exists a systematic motion of the stars, that it is exactly parallel to the plane of the Milky Way, and that the motion takes place in two exactly opposite directions, the two streams having a relative velocity of about
Since in the preceding theory the motion is introduced simply to explain certain centrifugal forces, it is at once evident that it supposes nothing about the direction in which the motion takes place. Nothing prevents us from assuming that part of the stars circulate one way, while the rest move in the opposite direction. The relative motion of the two groups will then evidently be
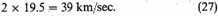
The motion to which our theory leads, besides being in the same plane, has therefore practically the exact value which is known from observation to exist. In fact we are led in the most direct and natural way to a complete explanation of the phenomenon of star-streaming. The circumstance that observation led us to assume two rectilinear streams, whereas we here find the motion to be circular, is probably unimportant. It is of course infinitely probable that the sun must be at a certain distance from the center of the system. If we suppose it to be at the point S (see figure 80.1) then the star-streams are derived from the observed motions of stars within a volume whose dimensions are of the order of those of the sphere around S shown in the figure. As long as the radius of this sphere is small in comparison with the distance of S from the center, the curvature of the stream-lines must be inappreciable.
When we consider that the value (27) has been obtained by a study of the arrangement of stars in space, in which the proper motions play no other part than that of a criterion of distance, while the value (26) has been obtained by a study of the motions themselves, both radial and transverse, the close agreement of the two results seems very significant. It becomes more so through the fact that both theories yield a motion exactly parallel to the plane of the Milky Way. Further, if we take into account the fact that the present theory leads to a value for the average mass of the stars which is in close accordance with what has also been found from utterly different investigations, and if we add a final point, namely, the natural explanation of the different arrangement of the stars of different spectral types, we are led irresistibly to the following conclusion:
The theory here propounded, though it may require considerable modification on account of its defectiveness both as to observational basis and mathematical treatment, is probably correct in its main features.
10, 11, 12, 13, 14 AND APPENDIX
Here we omit discussions of the velocity of escape of stars from the system, defects in the determinations of the rotational velocities, the exact position of the sun in the stellar system, and the fact that the solutions of this paper incorrectly assume that the stars form a heterogeneous collection. Also deleted is an appendix deriving the attraction of a homogeneous revolution ellipsoid on an exterior point.
1. E. C. Pickering and J. C. Kapteyn, Harvard-Groningen Durchmusterung of Selected Areas, Annals of the Harvard Observatory 101, 102, 103 (1918–1924); F. H. Seares, J. C. Kapteyn, and P. J. van Rhijn, "Mount Wilson Catalogue of Photographic Magnitudes in Selected Areas 1–139," Carnegie Institute of Washington Publication No. 402 (1930).
2. J. C. Kapteyn and P. J. van Rhijn, Astrophysical Journal 52, 23 (1920).
1. Astrophysical Journal 52, 23 (1920).
2. Mt. Wilson Contr., No. 229; Astrophysical Journal 55, 242 (1922).
3. Peculiar velocity is defined as the motion corrected for both the solar and stream-motion. The radial and transverse velocities agree in showing a certain excess of very large motions over the Maxwellian distribution. They are both represented satisfactorily by the sum of two Maxwellian distributions. A thorough separate treatment of all the spectral classes is still a great desideratum.
4. There is a mistake in the derivation of this value. The true value is certainly somewhat lower. From considerations given below I have not deemed it necessary for the present paper to repeat the computations with an improved value of
5. Monthly Notices 81, 4 (1920).
6. Jeans, Problems of Cosmogony and Stellar Dynamics (1919), p. 239.