Trigonometry

Somenumerical Problems in Mensuration

Hero of Alexandria, Metrica I. 8, III. 20, II. 12⁵

I. 8. There is a general method whereby, if the three sides of any triangle are given, it is possible to find the area without finding the altitude.

For example, let the sides of the triangle be of 7, 8, and 9 units.

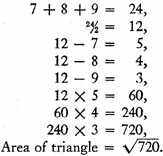¹

Now since 720 has no rational square root, we shall obtain a very close approximation to

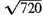
as follows:

The nearest [perfect integral] square to 720 is 729.

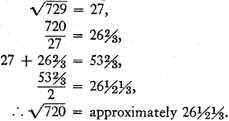
For

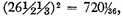
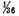
the difference being only of a unit.

Now if we desire that the difference be less than

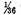
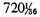
we commence with the number just obtained, instead of with 729, and by proceeding in the same way we shall find that the difference will be much less than 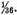²

III. 20. Let there be a pyramid, with base ABCD of any form, and vertex at point E, with side AE of 5 units. It is required to cut the pyramid by a plane parallel to the base in such a way that the pyramid cut off at the vertex is, let us say, four times the remaining solid. Let ZHTK be the section made by the cutting plane. Thus AZ will be a side of the solid ABCDZHTK.

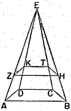
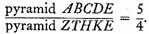
Now pyramids are to each other as the cubes of homologous sides.

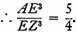
But

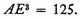
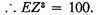
We must therefore find

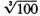
by approximation.

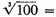
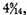
very nearly as we shall show below.

Thus if EZ be taken as

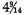
and the pyramid be cut at point Z by a plane parallel to the base, the problem is solved.

The synthesis is as follows.

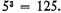
Since the ratio of the two parts is 4:1, we have

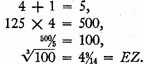
We shall now show how to find

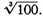
Take the cubic numbers nearest to 100, both greater and less, i.e., 125 and 64.

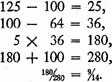
Adding

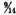
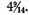
to the cube root of the smaller cubic number [64] we have This will be the approximation to 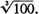¹

II. 12. Let it be required to measure the segment of a sphere, having a base of diameter 12 and height 2.¹

Now Archimedes proves that the ratio of a segment of a sphere to a cone with same base and equal height is equal to the ratio of the sum of the radius of the sphere and the height of the remaining segment, to the height of the remaining segment.²

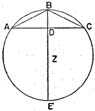
Let the segment in question be ABC, with altitude BD. Let Z be the center of the sphere.

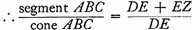
Since AC is given, AD and AD² are given.

That is,

is given.

But since BD is given, DE is also given, as is the whole of BE.

EZ is given, and also

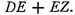
But since DE is given, the ratio of the cone, with base equal to the diameter of circle AC and height BD, to the segment of the sphere is also given.

The segment of the sphere is given.

We shall on the basis of this analysis proceed as follows:

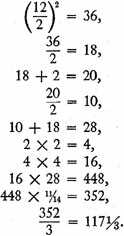
This will be the volume of the segment.

¹ This is an application of the so-called Heronian formula,

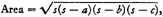
where a, b, and c are the sides and s half the perimeter. The geometrical proof is given both in the Metrica and in the Dioptra of Hero, but there is strong evidence that we owe the formula to Archimedes.

² The procedure is as follows:

Let

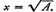
If x₁ is the first approximation, i.e., the square root of the nearest perfect square to A,

Let

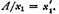
Now, the second approximation is the arithmetic mean of x₁ and

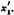
(1) That is

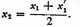
Similarly let

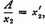
(2) and

and so on.

Hero, in the example given, does not go beyond equation (1). If the process is repeated we get, from equation (2),

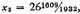
of which the square is

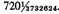
For a discussion of this method in connection with Archimedes’ approximation to

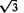
(p. 61, above), see T. L. Heath, History of Greek Mathematics II. 325.

¹ Precisely what general formula is applied in this procedure is not entirely clear. It has been suggested that the formula is

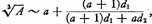
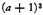
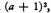
where a³ and are the nearest perfect cubes below and above A, and d₁ and d₂ the differences between A and a³, and A and respectively. For a discussion see T. L. Heath, op. cit., II. 341.

¹ The reference evidently is to a segment of one base.

² Archimedes, On the Sphere and the Cylinder II, Prop. 2, Corollary.