Mathematics

12 BERKELEY.

The Analyst

3 The Method of Fluxions is the general key by help whereof the modern mathematicians unlock the secrets of Geometry, and consequently of Nature. And, as it is that which hath enabled them so remarkably to outgo the ancients in discovering theorems and solving problems, the exercise and application thereof is become the main if not sole employment of all those who in this age pass for profound geometers. But whether this method be clear or obscure, consistent or repugnant, demonstrative or precarious, as I shall inquire with the utmost impartiality, so I submit my inquiry to your own judgment, and that of every candid reader. Lines are supposed to be generated by the motion of points, planes by the motion of lines, and solids by the motion of planes. And whereas quantities generated in equal times are greater or lesser according to the greater or lesser velocity wherewith they increase and are generated, a method hath been found to determine quantities from the velocities of their generating motions. And such velocities are called fluxions: and the quantities generated are called flowing quantities. These fluxions are said to be nearly as the increments of the flowing quantities, generated in the least equal particles of time; and to be accurately in the first proportion of the nascent, or in the last of the evanescent increments. Sometimes, instead of velocities, the momentaneous increments or decrements of undetermined flowing quantities are considered, under the appellation of moments.

4 By moments we are not to understand finite particles. These are said not to be moments, but quantities generated from moments, which last are only the nascent principles of finite quantities. It is said that the minutest errors are not to be neglected in mathematics:¹ that the fluxions are celerities, not proportional to the finite increments, though ever so small; but only to the moments or nascent increments, whereof the proportion alone, and not the magnitude, is considered. And of the aforesaid fluxions there be other fluxions, which fluxions of fluxions are called second fluxions. And the fluxions of these second fluxions are called third fluxions: and so on, fourth, fifth, sixth, &c. ad infinitum. Now, as our sense is strained and puzzled with the perception of objects extremely minute, even so the imagination, which faculty derives from sense, is very much strained and puzzled to frame clear ideas of the least particles of time, or the least increments generated therein: and much more so to comprehend the moments, or those increments of the flowing quantities in statu nascenti, in their very first origin or beginning to exist, before they become finite particles. And it seems still more difficult to conceive the abstracted velocities of such nascent imperfect entities. But the velocities of the velocities, the second, third, fourth, and fifth velocities, &c., exceed, if I mistake not, all human understanding. The further the mind analyseth and pursueth these fugitive ideas the more it is lost and bewildered; the objects, at first fleeting and minute, soon vanishing out of sight. Certainly in any sense, a second or third fluxion seems an obscure mystery. The incipient celerity of an incipient celerity, the nascent augment of a nascent augment, i.e., of a thing which hath no magnitude: take it in what light you please, the clear conception of it will, if I mistake not, be found impossible; whether it be so or no I appeal to the trial of every thinking reader. And if a second fluxion be inconceivable, what are we to think of third, fourth, fifth fluxions, and so on without end?

5 The foreign mathematicians are supposed by some, even of our own, to proceed in a manner less accurate, perhaps, and geometrical, yet more intelligible. Instead of flowing quantities and their fluxons, they consider the variable finite quantities as increasing or diminishing by the continual addition or subduction of infinitely small quantities. Instead of the velocities wherewith increments are generated, they consider the increments or decrements themselves, which they call differences, and which are supposed to be infinitely small. The difference of a line is an infinitely little line; of a plane an infinitely little plane. They suppose finite quantities to consist of parts infinitely little, and curves to be polygons, whereof the sides are infinitely little, which by the angles they make one with another determine the curvity of the line. Now to conceive a quantity infinitely small, that is, infinitely less than any sensible or imaginable quantity, or than any the least finite magnitude is, I confess, above my capacity. But to conceive a part of such infinitely small quantity that shall be still infinitely less than it, and consequently though multiplied infinitely shall never equal the minutest finite quantity, is, I suspect, an infinite difficulty to any man whatsoever; and will be allowed such by those who candidly say what they think; provided they really think and reflect, and do not take things upon trust.

6 And yet in the calculus differentialis, which method serves to all the same intents and ends with that of fluxions, our modern analysts are not content to consider only the differences of finite quantities: they also consider the differences of those differences, and the differences of the differences of the first differences. And so on ad infinitum. That is, they consider quantities infinitely less than the least discernible quantity; and others infinitely less than those infinitely small ones; and still others infinitely less than the preceding infinitesimals, and so on without end or limit. Insomuch that we are to admit an infinite succession of infinitesimals, each infinitely less than the foregoing, and infinitely greater than the following. As there are first, second, third, fourth, fifth, &c. fluxions, so there are differences, first, second, third, fourth, &c., in an infinite progression towards nothing, which you still approach and never arrive at. And (which is most strange) although you should take a million of millions of these infinitesimals, each whereof is supposed infinitely greater than some other real magnitude, and add them to the least given quantity, it shall never be the bigger. For this is one of the modest postulata of our modern mathematicians, and is a corner-stone or ground-work of their speculations.

. . . . . . .

9 Having considered the object, I proceed to consider the principles of this new analysis by momentums, fluxions, or infinitesimals; wherein if it shall appear that your capital points, upon which the rest are supposed to depend, include error and false reasoning; it will then follow that you, who are at a loss to conduct your selves, cannot with any decency set up for guides to other men. The main point in the method of fluxions is to obtain the fluxion or momentum of the rectangle or product of two indeterminate quantities. Inasmuch as from thence are derived rules for obtaining the fluxions of all other products and powers; be the coefficients or the indexes what they will, integers or fractions, rational or surd. Now, this fundamental point one would think should be very clearly made out, considering how much is built upon it, and that its influence extends throughout the whole analysis. But let the reader judge. This is given for demonstration. Suppose the product or rectangle AB increased by continual motion: and that the momentaneous increments of the sides A and B are a and b. When the sides A and B were deficient, or lesser by one haft of their moments, the rectangle was

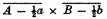
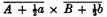
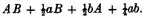
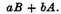
i.e., And as soon as the sides A and B are increased by the other two halves of their moments, the rectangle becomes or From the latter rectangle subduct the former, and the remaining difference will be Therefore the increment of the rectangle generated by the intire increments a and b is 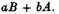Q.E.D. 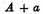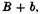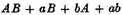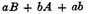But it is plain that the direct and true method to obtain the moment or increment of the rectangle AB, is to take the sides aa increased by their whole increments, and so multiply them together, by the product whereof is the augmented rectangle; whence, if we subduer AB the remainder will be the true increment of the rectangle, exceeding that which was obtained by the former illegitimate and indirect method by the quantity ab. And this holds universally be the quantities a and b what they will, big or little, finite or infinitesimal, increments, moments, or velocities. Nor will it avail to say that ab is a quantity exceeding small: since we are told that in rebus mathematicis errores quam minimi non sunt contemnendi.²

10 Such reasoning as this for demonstration, nothing but the obscurity of the subject could have encouraged or induced the great author of the fluxionary method to put upon his followers, and nothing but an implicit deference to authority could move them to admit. The case indeed is difficult. There can be nothing done till you have got rid of the quantity ab. In order to this the notion of fluxions is shifted: It is placed in various lights: Points which should be clear as first principles are puzzled; and terms which should be steadily used arc ambiguous. But notwithstanding all this address and skill the point of getting rid of ab cannot be obtained by legitimate reasoning. If a man, by methods not geometrical or demonstrative, shall have satisfied himself of the usefulness of certain rules; which he afterwards shall propose to his disciples for undoubted truths; which he undertakes to demonstrate in a subtile manner, and by the help of nice and intricate notions; it is not hard to conceive that such his disciples may, to save themselves the trouble of thinking, be inclined to confound the usefulness of a rule with the certainty of a truth, and accept the one for the other; especially if they are men accustomed rather to compute than to think; earnest rather to go on fast and far, than solicitous to set out warily and see their way distinctly.

35 I know not whether it be worth while to observe, that possibly some men may hope to operate by symbols and suppositions, in such sort as to avoid the use of fluxions, momentums, and infinitesimals, after the following manner. Suppose x to be an absciss of a curve, and z another absciss of the same curve. Suppose also that the respective areas are xxx and zzz: and that

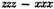
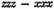
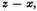
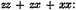
the increment of the absciss, and the increment of the area, without considering how great or how small these increments may be. Divide now by and the quotient will be and, supposing that z and x are equal, this same quotient will be 3xx, which in that case is the ordinate, which therefore may be thus obtained independently of fluxions and infinitesimals. But herein is a direct fallacy: for, in the first place, it is supposed that the abscisses z and x are unequal, without which supposition no one step could have been made; and in the second place, it is supposed they are equal; which is a manifest inconsistency, and amounts to the same thing that hath been before considered. And there is indeed reason to apprehend that all attempts for setting the abstruse and fine geometry on a right foundation, and avoiding the doctrine of velocities, momentums, &c. will be found impracticable, till such time as the object and end of geometry are better understood than hitherto they seem to have been. The great author of the method of fluxions felt this difficulty, and therefore he gave into those nice abstractions and geometrical metaphysics without which he saw nothing could be done on the received principles; and what in the way of demonstration he hath done with them the reader will judge. It must, indeed, be acknowledged that he used fluxions, like the scaffold of a building, as things to be laid aside or got rid of as soon as finite lines were found proportional to them. But then these finite exponents are found by the help of fluxions. Whatever therefore is got by such exponents and proportions is to be ascribed to fluxions: which must therefore be previously understood. And what are these fluxions? The velocities of evanescent increments? And what are these same evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?³

¹ We recognize the statement made by Newton in his Quadratura curvarum (Selection V.7).

² Newton’s statement again, this time in Latin.

³ We may think here of the many arguments involved in the Zeno paradoxes, which also played a role in the eighteenth-century discussions concerning the foundations of the calculus; see Cajori, History of the conceptions of limits and fluxions, quoted in the introduction to this selection, and his nine articles, "History of Zeno’s arguments on motion," American Mathematical Monthly 22 (1915).