Mathematics

39b. Roch on the Riemann-Roch Theorem¹

If w is an algebraic function, defined by the [irreducible polynomial] equation

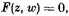
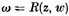
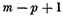
then any function ω having the same ramifications as w ["wie w verzweigte"] can be expressed as a rational function of w and z.² If ω has simple infinities ["wird ω unendlich erster Ordnung"] at the m branch points of its [Riemann] surface T, then by §5 of Riemann 39a [the expression for] ω contains arbitrary constants. 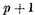Already Riemann’s condition for the existence of functions becoming infinite in fewer than points shows that the number of essential ["wirklich vorhandenen"] constants can be greater.

However, this can also be the case when

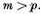
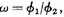
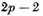
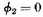
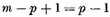
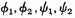
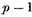
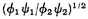
For example, if then ω becomes infinite in the points where (see §10 of Riemann’s paper),³ and contains as many arbitrary constants as φ₁, namely p, whereas in this case. On the other hand, if are four functions which are infinitesimals of the second order at points, whose square roots Riemann calls "Abelian functions," then there exist [a certain number of] expressions which are rational functions of z and w. 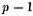These indeed depend linearly on parameters, a theorem stemming from Riemann which is a special case of the following result.

The most general Abelian integral of the second kind, which becomes simply infinite at m points e_j, is

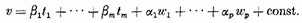
(see [39a], §5). Here

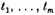
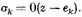
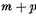
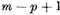
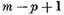
are special [Abelian] integrals of the second kind which become infinite like where In order for v to become algebraic, its moduli of periodicity must vanish.⁴ This gives 2p linear equations to be satisfied by the constants β_k and α_l, thus leaving arbitrary constants. Only if these 2p equations are linearly independent can ω contain more than constants.

To investigate this possibility, we let the special expressions

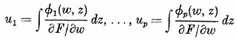
be the nowhere infinite ["endlich bleibende"] integrals introduced by Riemann as arguments for his θ-function. The integral u_μ has the modulus of periodicity πi across the cut α_μ, and moduli of periodicity zero across the other

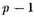
cuts a_k, and across the cuts b_v the moduli of periodicity a_{μ, v-} Near the point e_k, let us suppose that

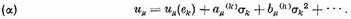
In general—that is, when the e_k are neither at ∞ nor branch points—we have

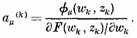
The [Abelian] integrals of the second kind can be so chosen that their moduli of periodicity vanish across the cuts α_μ. For, given t_k with the moduli

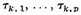
across these cuts, one need only set

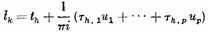
to get t_k with the desired properties. This reduces the conditions for the moduli of periodicity of the expression

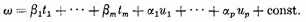
to vanish across the cuts α_μ to the equations

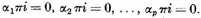
The remaining constants β correspond simply to the p conditions for the moduli of periodicity to vanish across the cuts b_v, as will be explained below.

The whole ["ganze"] integral ∫ u_μ dv extended over the bounded, simply connected domain formed from T by taking its cuts α_μ and b_v as boundaries is equal to

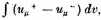
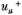
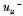
where and are the values of u_μ . on the positive and negative sides of the cuts. This gives [Roch sketches the reasoning]

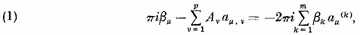
which, since μ ranges over the integers

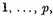
gives p equations which express the dependence of the moduli of periodicity on the points e_k.

From now on, we shall assume for simplicity that all e_k are finite and that none is a branch point. This reduces (1) to

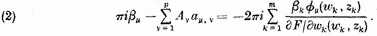
This formula transforms the p equations

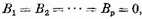
noted above, into

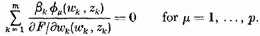
These equations are linearly dependent if and only if one can so choose coefficients

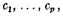
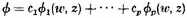
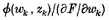
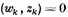
in [the expression] that for

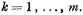
This is the condition on

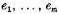
which permits φ to vanish at all branch points other than the r coincident ones.⁵ Nevertheless, two or more of the p equations can follow from the others, and the general result can be stated as follows:

If a function w has in simple poles, and if q linearly independent functions

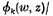
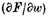can vanish at these poles, then ω depends on 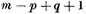arbitrary constants.

For example, let

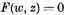
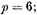
be the equation of a quintic curve. Then in general, that is, unless the curve has a double point, the integrals remaining bounded are

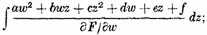
hence every quadratic polynomial function is [such] a function φ_k. The function

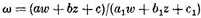
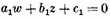
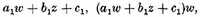
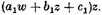
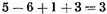
has poles at the five points where the straight line intersects the given curve. At these five points, three linearly independent functions φ vanish, namely: and Hence ω contains arbitrary constants: a, b, and c.

If the given quintic curve has a double-point, then

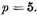
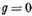
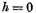
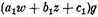
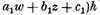
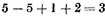
Hence, if and represent two straight lines passing through the double-point, only and are functions φ which are zero at the five points where ω becomes infinite, and ω again contains constants.

If some of the points e_k are infinite, then one must ask about the number of [linearly independent] functions which are of lower degree than the highest possible one and which vanish at the points e_k which lie in the finite plane. [The result is:]

Let

be the constants in question, and let those [Abelian] integrals which remain bounded be represented by the series (α). Let there exist q linearly independent functions

which vanish at the in points e_k. Then an algebraic function which becomes simply infinite at the points e_kcontains

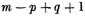arbitrary constants.

[Roch concludes by sketching a way to treat higher-order infinities, and observing that his formula (1) generalizes an earlier formula of Weierstrass for hyperelliptic integrals.]

¹ G. Roch "Uber die Anzahl willkürlichen Constanten in algebraischen Funktionen," J. reine ang. Math. 64 (1864), 372–376.

² Roch wrote s, s′ where we have written w, ω.

³ Roch here refers to the paper by Riemann from which Selection 39a is taken.

⁴ "Damit v in eine algebraische Funktion übergehe, müssen sämmtliche Periodicitätsmoduln yon v verschwinden." Today, "moduli of periodicity" are called "periods."

⁵ "oder wenn die m Punkte e_k solche sind, in denen amuser den r zusammengefallenen sich auf-hebenden Verzweigungspunkte ... φ verschwinden kann."