The Steady-State Theory of the Expanding Universe

Hermann Bondi and Thomas Gold

(Monthly Notices of the Royal Astronomical Society 108, 252–270 [1948])

Summary—The applicability of the laws of terrestrial physics to cosmology is examined critically. It is found that terrestrial physics can be used unambiguously only in a stationary homogeneous universe. Therefore a strict logical basis for cosmology exists only in such a universe. The implications of assuming these properties are investigated.

Considerations of local thermodynamics show as clearly as astronomical observations that the universe must be expanding. Hence, there must be continuous creation of matter in space at a rate which is, however, far too low for direct observation. The observable properties of such an expanding stationary homogeneous universe are obtained, and all the observational tests are found to give good agreement.

The physical properties of the creation process are considered in some detail, and the possible formulation of a field theory is critically discussed.

1. THE PERFECT COSMOLOGICAL PRINCIPLE

THE UNRESTRICTED REPEATABILITY of all experiments is the fundamental axiom of physical science. This implies that the outcome of an experiment is not affected by the position and the time at which it is carried out. A system of cosmology must be principally concerned with this fundamental assumption and, in turn, a suitable cosmology is required for its justification. In laboratory physics we have become accustomed to distinguish between conditions which can be varied at will and the inherent laws which are immutable.

Such a distinction between the "accidental" conditions and the "inherent" laws and constants of nature is justifiable so long as we have control over the "accidental," and can test the validity of the distinction by a further experiment. In astronomical observations we do not have this control, and we can hence never prove which is "accidental" and which "inherent." This difficulty, though logically a very real one, need not concern us in an interpretation of the dynamics of the solar system. We may be satisfied when we discover that the solar system with all its numerous orbits is accurately one of the many systems permitted by our "inherent" laws.

But when we wish to consider the behaviour of the entire universe, then the logical basis for a distinction between "inherent" laws and "accidental" conditions disappears. Any observation of the structure of the universe will give as unique a result as, for instance, a determination of the velocity of light or the constant of gravitation. And yet, if we were to contemplate a changing universe we should have to assume some such observations to represent "accidental" conditions and others "inherent" laws.

Such assumptions were in fact implied in all theories of evolution of the universe; they were necessary to specify the problem. Without them, there would be no rules and hence unlimited freedom in any extrapolation into the future or into the past. Some such sets of assumptions may be intellectually much more satisfying than others, and accordingly they are adopted. We may place much reliance in such aesthetic judgments, but we cannot claim any logical foundation for them.

1.2. Let us take an example to demonstrate the point of this criticism. Present observations indicate that the universe is expanding. This suggests that the mean density in the past has been greater than it is now. If we are now to make any statement regarding the behaviour of such a denser universe, and the way in which it is supposed to have reached its present condition, then we have to know the physical laws and constants applicable in denser universes. But we have no determinations for those. An assumption which is commonly made is to say that those physical laws which we have learnt to regard as "intrinsic" because they are unaffected by any changes of conditions which we may produce, are in fact not capable of any change. It is admitted that such a change of the density of the universe would have slight local effects; there would be more or less light arriving here from distant galaxies. But, it is assumed, there would be no change in the physical laws which an observer would deduce in a laboratory.

Such a philosophy may be intellectually very agreeable: it gives permanence to the abstract things, the physical laws, whilst it regards the present condition of the universe as merely a particular demonstration of the consequences of such laws. There are, however, grave difficulties inherent in such a view. The most striking of those is concerned with the absolute state of rotation of a body. Mach¹ examined this problem very thoroughly and all the advances in theory which have been made have not weakened the force of his argument. According to "Mach’s Principle" inertia is an influence exerted by the aggregate of distant matter which determines the state of motion of the local frame of reference by means of which rotation or acceleration is measured. A particular rotational state which is described as "nonrotating" can be found by a purely local experiment (a Foucault pendulum, for instance). This rotational state is always found to coincide accurately with the rotational state of the distant stars around the observer. Mach’s principle is the recognition that this coincidence must in fact be due to a causal relation. If, as is now widely agreed, we adopt Mach’s principle, then we imply that the nature of any local dynamical experiment is fundamentally affected by distant matter. We can hence not contemplate a laboratory which is shielded so as to exclude all influence from outside: and for the same reason we cannot have any logical basis for choosing physical laws and constants and assigning to them an existence independent of the structure of the universe.

Any interdependence of physical laws and large-scale structure of the universe might lead to a fundamental difficulty in interpreting observations of light emitted by distant objects. For if the universe, as seen from those objects, presented a different appearance, then we should not be justified in assuming familiar processes to be responsible for the emission of the light which we analyse. This difficulty is partly removed by the "cosmological principle." According to this principle all large-scale averages of quantities derived from astronomical observations (i.e. determination of the mean density of space, average size of galaxies, ratio of condensed to uncondensed matter, etc.) would tend statistically to a similar value independent of the positions of the observer, as the range of the observation is increased; provided only that the observations from different places are carried out at equivalent times. This principle would mean that there is nothing outstanding about any place in the universe, and that those differences which do exist are only of local significance; that seen on a large scale the universe is homogeneous.

This principle is widely recognized, and the observations of distant nebulae have contributed much evidence in its favour. An analysis of these observations indicates that the region surveyed is large enough to show us a fair sample of the universe, and that this sample is homogeneous.

But in the sense in which the principle came to be adopted there is the qualification regarding the time of the observation. The universe is still presumed to be capable of altering its large-scale structure, but only in such a way as not to upset its homogeneity. The result of a large-scale observation may hence be a measure of a universal time.

We might have looked to the cosmological principle for a justification of the assumption of the general validity of physical laws; but whilst the principle supplies the justification with respect to changes of place, it still leaves the possibility of a change of physical laws with universal time. Any system of cosmology must still involve a speculation about this dependence as one of its basic assumptions. Indced, we are not even in a position to interpret observations of very distant objects without such an assumption, for the light which we receive from them was emitted at a different instant in this scale of universal time, and accordingly the processes responsible for its emission may be unfamiliar to us.

The systems of cosmology may well be classified according to the assumption made or implied at this stage of the argument. While one school of thought considers all the results of laboratory physics to be always applicable, without regard to the state of the universe, another starts from the narrow cosmological principle and with the aid of a number of intellectually agreeable assumptions arrives at the conclusion that laboratory physics is qualitatively permanently valid, though some of its "constants" are changing. There are yet other schools of thought which attempt to distinguish the changeable from the permanent constants by their magnitudes.

We shall proceed quite differently at this point. As the physical laws cannot be assumed to be independent of the structure of the universe, and as conversely the structure of the universe depends upon the physical laws, it follows that there may be a stable position. We shall pursue the possibility that the universe is in such a stable, self-perpetuating state, without making any assumptions regarding the particular features which lead to this stability. We regard the reasons for pursuing this possibility as very compelling, for it is only in such a universe that there is any basis for the assumption that the laws of physics are constant; and without such an assumption our knowledge, derived virtually at one instant of time, must be quite inadequate for an interpretation of the universe and the dependence of its laws on its structure, and hence inadequate for any extrapolation into the future or the past.

Our course is therefore defined not only by the usual cosmological principle but by that extension of it which is obtained on assuming the universe to be not only homogeneous but also unchanging on the large scale. This combination of the usual cosmological principle and the stationary postulate we shall call the perfect cosmological principle, and all our arguments will be based on it. The universe is postulated to be homogeneous and stationary in its large-scale appearance as well as in its physical laws.

We do not claim that this principle must be true, but we say that if it does not hold, one’s choice of the variability of the physical laws becomes so wide that cosmology is no longer a science. One can then no longer use laboratory physics without relying on some arbitrary principle for their extrapolation.

But if the perfect cosmological principle is satisfied in our universe then we can base ourselves confidently on the permanent validity of all our experiments and observations and explore the consequences of the principle. Unless and until any disagreement appears we therefore accept the principle, since this is the only assumption on the basis of which progress is possible without further hypothesis. As will be seen later many conclusions can be drawn which can be compared with experiment. It would be most fortuitous if no contradictions arose, although the perfect cosmological principle was not valid.

2. APPLICATION OF THE PERFECT COSMOLOGICAL PRINCIPLE

2.1. Although the perfect cosmological principle states that the universe is homogeneous and stationary on the large scale no statement is made about spatial isotropy. This is usually assumed together with homogeneity for mathematical convenience, but in our view the position of the two assumptions is quite different. Homogeneity and the stationary property are vital to the very existence of the subject. There may be similarly strong arguments for isotropy, but those so far advanced do not seem to us to be equally compelling. Further considerations of the nature of the stable self-perpetuating state referred to above can be made, which suggest but do not prove isotropy.

We shall therefore introduce spatial isotropy as an assumption which is strongly suggested both by local and by astronomical observations and which is simplest.

We must now apply the perfect cosmological principle to laboratory physics and to astronomical observations. We regard the principle as of such fundamental importance that we shall be willing if necessary to reject theoretical extrapolations from experimental results if they conflict with the perfect cosmological principle even if the theories concerned are generally accepted. Of course we shall never disregard any direct observational or experimental evidence and we shall see that we can easily satisfy all such requirements.

2.2. For the perfect cosmological principle to apply, one might at first sight expect that the universe would have to be static, i.e. to possess no consistent large-scale motion. This, however, would conflict with the observations of distant galaxies, and it would also conflict with the thermodynamic state which we observe. For such a static universe would be very different indeed from the universe we know. A static universe would clearly reach thermodynamical equilibrium after some time. An infinitely old universe would certainly be in this state. There would be complete equilibrium between matter and radiation, and (apart possibly from some slight variations due to gravitational potentials) everything would be at one and the same temperature. There would be no evolution, no distinguishing features, no recognizable direction of time. That our universe is not of this type is clear not only from astronomical observations but from local physics and indeed from our very existence. Accordingly there must be large-scale motions in our universe. The perfect cosmological principle permits only two types of motion, viz. large-scale expansion with a velocity proportional to distance, and its reverse, large-scale contraction.

In a contracting universe there would be even more radiation compared with matter than in a static universe. Therefore we reject this possibility and confine our attention to an expanding universe.

2.3. The observations of distant galaxies, which are now capable of a more rigorous interpretation by means of the perfect cosmological principle, inform us of the notion of expansion. This motion in which the velocity is proportional to the distance (apart from a statistical scatter) is well known to be of the only type compatible with homogeneity; but the compatibility with the hypothesis of a stationary property requires investigation. If we considered that the principle of hydrodynamic continuity were valid over large regions and with perfect accuracy then it would follow that the mean density of matter was decreasing, and this would contradict the perfect cosmological principle. It is clear that an expanding universe can only be stationary if matter is continuously created within it. The required rate of creation, which follows simply from the mean density and the rate of expansion, can be estimated as at most one particle of proton mass per litre per 10⁹ years. In interpreting the universe as stationary we have to assume that such a process of creation is operative: we have to infringe the principle of hydrodynamic continuity. But this principle is not capable of experimental verification to such a precision, and this infringement does not constitute a contradiction with observational evidence. It is true that hydrodynamic continuity has been regarded as an unqualified truth and not as an approximation to physical laws, but this was merely a bold simplifying extrapolation from evidence. Hydrodynamic continuity is no doubt approximately true but this does not compel us to assume that it holds without any deviation whatever. In the conflict with another principle which is much more far-reaching and capable of making many more statements about the nature of the universe and the applicability of physical laws, there is no reason for upholding the principle of continuity to an indefinite accuracy, far beyond experimental evidence.

We have referred to the principle infringed by the creation process as the principle of hydrodynamic continuity; as we shall see later it is by no means clear whether we can regard any principle of conservation of energy as infringed.

2.4. Much of the structure of the universe is closely defined by the perfect cosmological principle and the knowledge of the velocity-distance law of expansion. As we shall see later such a universe must be described by a de Sitter metric. The universe is therefore spatially as well as temporally infinite, but the effect of distant matter on an observer tends to zero as its velocity of recession approaches the velocity of light.

The motion of matter in such a universe follows a particular pattern; though in the actual case there are fluctuations, there is a preferred motion defined at each place. Any observer equipped with a sufficiently good telescope can make observations of the velocity-distance law in different directions, and from such observations he can deduce any deviation that he may have from this preferred motion in his locality. If he follows this motion without any deviation then he will see symmetry around him; although all the objects which he observes may have some deviations from the preferred motions in their localities, a statistical averaging method can serve to specify the preferred motion at the observer exactly. (It is not necessary to specify the averaging method at this point beyond stating that it must give sufficient weight to distant matter.) At any rate there is not much latitude. Such a preferred motion could be established by an observer at any place, and the resulting pattern forms a vector field in a four dimensional space-time. Much physical significance must be attached to this vector-field, for the motion of all matter appears to be closely dictated by it. What deviations there are, are statistically distributed around the preferred motion, and these deviations are quite small compared with the velocity of light.

An interesting problem connected with the preferred direction is that of the existence of a "cosmic time." In the cosmologies of general relativity the existence of a cosmic time is deduced from Weyl’s postulate.² As observations show, there are irregularities and deviations from uniformity. These are only small, but if they are such that there are no surfaces orthogonal to the world lines of all the nebulae, then there is no cosmic time. The existence of a cosmic time in the presence of these irregularities has not been proved and seems improbable. The ambiguities in cosmic time arising from such a breakdown are only small in any region, but over the universe as a whole they completely undermine the logical structure on which a homogeneous but not stationary theory rests. Our position is very different. Owing to the stationary character of the universe, homogeneity can be defined in the absence of cosmic time. Whether or not there are surfaces orthogonal to the preferred direction is therefore of no importance for our theory. On general grounds one would not expect these surfaces to exist, so that an unambiguous definition of cosmic time is impossible. In the simplified smoothed-out model it will of course exist, but probably not in the actual universe with its irregularities.

The stationary property implies that the factor of the velocity-distance law must stay constant. This would not be fulfilled if matter moved such that the velocity between two particular masses remained constant; the velocity has to increase as the distance increases. Accordingly, there must be relative acceleration between matter.

We can now examine the requirements which the perfect cosmological principle places on the evolution of stars and galaxies. The mean ratio of condensed to uncondensed matter has to stay constant, and for this reason new galaxies have to be formed as older ones move away from each other. We take the perfect cosmological principle to imply that no feature of the universe is subject to any consistent change, and no observer hence capable of any unique definition of a universal time. This will be satisfied only if the ages of galaxies in any sufficiently large volume follow a certain statistical distribution. With such a distribution it is of course possible for any particular volume to contain a very old galaxy; but very old galaxies are thinly scattered, as they have had time to move far apart in the general expansion. The characteristic time in this age distribution must of course be related to the characteristic time of expansion of the universe. In opposition to most other theories we should hence expect to find much diversity in the appearance of galaxies, as they will be of greatly different ages; and much diversity is in fact observed. Furthermore the age distribution of galaxies in any volume will be independent of the time of observation, and it will hence be the same for distant galaxies as for near ones, although in the former case the light has taken long to reach us. This is a property of great importance, for it is in practice the only basis on which we can construct any interpretation of the observations of distant galaxies.

2.5. The next point to discuss is the thermodynamic state of the universe. It is known that this state is very far from any equilibrium. Very much more energy is in the form of matter than in radiation; and very much more energy is radiated away than is absorbed by matter.

The disequilibrium is very great indeed, and we have grown so used to it that we take its existence to be self-evident. Such statements as "A hydrogen atom in an excited state returns quickly to its ground state, since this has less energy", do not indicate any lack of faith in the principle of conservation of energy but merely an awareness of the paucity of radiation in the universe which makes the reverse process so very unlikely.

This disequilibrium is such a marked and characteristic feature of our universe that its explanation must be one of the main tasks of cosmology. The connection between this phenomenon and cosmology was noticed by Olbers³, who pointed out that in an infinite homogeneous static Newtonian universe the mean radiation density would be as high as it is on the surface of a star! In the present case, however, this disequilibrium is the direct consequence of the motion of expansion. Any photon emitted by a star has a very large probable free path, owing to the tenuous distribution of opaque matter in the universe. The most likely career for such a photon is that it will travel on into regions where the local motion of matter is very different from the motion of the star which caused its emission. When such a photon is finally absorbed, then it will, as seen by an observer on the absorbing matter, be subject to a Doppler-shift which reduces its frequency by a large factor. The thermal energy it will supply to the intercepting matter will hence be only a small fraction of the energy it removed from the emitting star. It is not necessary to consider here whether the difference in energy can be regarded as being supplied to the expansion process of the universe; but it is clear that the universe provides in this way a sink for radiative energy, and that this sink is in fact available to the majority of photons produced at the surface of stars. The process of getting rid of both matter and radiation from any fixed volume is by pushing both across the surface bounding this volume; and both are replenished from within.

It is of course important for any theory of cosmology that it should not predict thermodynamic equilibrium, and this is possible only by supposing either that insufficient time has been available since the commencement of radiation by stars, or, and this is the view we take, by suggesting that the bulk of the energy radiated does not again become available as heat.

A thermodynamic disequilibrium is a requirement for any local thermodynamical evolution, and in this sense it is necessary in order that any physical significance should be attached to the passage of time. In a stationary universe this condition can be fulfilled only if there is a motion of expansion, and if the mean free path of a photon is at least comparable with the dimension defined by the velocity-distance law and the velocity of light. (The radius of a de Sitter universe.) Expressing the same consideration differently: the perfect cosmological principle and the knowledge of the thermodynamic disequilibrium require that the universe should be expanding. The experimental evidence of the recession of nebulae is hence a good indication that this specific requirement of the perfect cosmological principle is in fact satisfied. The narrow cosmological principle would have resulted in no such requirement, for there the disequilibrium would result simply if the luminosity of all stars was a suitable function of universal time.

Let us now consider the question of the overall conservation of mass (energy) in such a universe. An observer attempting to estimate the quantity of matter in the universe will find that his result depends on the threshold intensities and wavelengths of his apparatus. Keeping these fixed, he will always observe a finite amount of matter and this will be constant in time. At a great range matter is drifting into an unobservable state by approaching the velocity of light, and without a process of creation this would not allow any principle of conservation of energy to be applied to the sum total of all observable matter.

A further point to be mentioned in relation to the stationary property of the universe is the coincidence of numbers pointed out by Eddington.⁴ Two non-dimensional numbers which can be constructed from observation are both found to be of the order 10³⁹; one is the ratio of the characteristic length defining the expansion of the universe to the classical radius of the electron (e²/mc²), and the other is the ratio of the electric to the gravitational force between a proton and an electron. The coincidence is striking, and though we have no causal connection to offer we feel that one exists. This and some other coincidences cannot be ignored by a system of cosmology to the extent of suggesting that they occur only in a fleeting phase. It is satisfactory that according to the theory presented here such coincidences are permanent.

3. THE OBSERVATIONAL TESTS

3.1. Our observations of the universe depend on the interactions between the rest of the universe and ourselves. These interactions are of two kinds: dynamical and electromagnetic. Dynamically, the rest of the universe affects us primarily through the long-range force of inertia, i.e. it defines inertial frames of reference in our neighbourhood. This dynamical interaction is strong and arises almost certainly from the whole of the observable universe, but it is ill-understood and is discussed in other parts of this paper. Therefore, in this section we shall confine ourselves to a discussion of the electromagnetic interactions, which are more easily interpreted.

Light reaches us in observable intensities from large numbers of extragalactic nebulae, and a considerable amount of information has been gathered. In particular the distribution over the sky and the number of nebulae of given apparent magnitude is quite well known, and the radial velocities have been determined (from the Doppler shift) for many nebulae.

In trying to interpret these data, we must first decide whether the observations extend over a sufficiently large region to have any bearing on cosmology, or whether they must be taken to refer to a purely local district.

There are two strong arguments (isotropy and homogeneity of nebular distribution and magnitude of the radial velocities), for assuming that the observations cover a fair sample of the universe and there is no evidence against it. In common with most writers on the subject we assume therefore that the observations refer to a sufficiently large region to be of relevance to cosmology.

3.2. We must now see whether our theory, at this stage of its development, can make any statements about the aspect of the universe which can be compared with observation. The mathematical apparatus we can use is strictly limited, since the field equations of the general theory of relativity with their insistence on conservation of mass are clearly not acceptable to us. In fact we must rely largely on kinematical arguments and on the generally accepted results of laboratory physics dealing with the propagation of light (special theory of relativity). The power of these kinematical arguments was demonstrated by the pioneer work of Milne and by the papers of Walker and Robertson.

A simplified model of the universe can be obtained by assuming the conditions of homogeneity and isotropy to be absolutely (instead of only on a large scale) satisfied. There seems to be good reason to believe that the features amenable to long distance observation are nearly the same in this simplified model as in the actual universe with all its irregularities. In common with most authors we shall assume that this representation of the universe is sufficient for comparison with the observations of extragalactic nebulae.

The mathematical properties of such a model have been studied in great detail by Robertson⁵ and by Walker.⁶ These authors adopt a narrower cosmological principle and they do not assume a stationary property. They do, however, assume that the particle paths do not intersect except that possibly they all intersect at one singular point in the past (origin of universe). Although we do not wish to make this assumption in general it is clear that in the simple model we are now discussing the assumption will be satisfied. For if there were an intersection at a point P, then the isotropy condition would show that this point had to be a focus, and the homogeneity condition would then lead us to a universe in which every point is a focus. Such a universe is evidently so different from the one we know that we need not hesitate to reject this possibility.

Accordingly, the work of Robertson and Walker is applicable to our theory, except that we have to specialize their results by the stationary condition. In this way the following theorem can be established:

In a non-static stationary universe the light-paths are the null geodesics of the metric

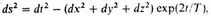
where the (x, y, z) coordinates of any particle partaking of the general motion of the universe are constant and t measures the proper time of any observer travelling with such a particle. T is a universal constant and the velocity of light has been put equal to unity. This metric is very well known, having been discovered by de Sitter⁷ in 1917. It is the simplest of all metrics of the Robertson type, but could not be used in general relativity, since the field equations imply that it describes empty space only.

The geometrical properties of the de Sitter universe are very simple. If we change from Cartesians (x, y, z) to spherical polars (r, θ, Φ) in the usual way, then an observer at the origin would find that the spectral lines of a source of light of luminosity L at (r, θ, Φ) received by him at time

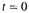
would show a red shift

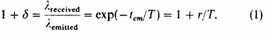
while the intensity of light received would be

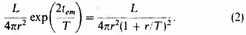
These results are well known⁸ and apply equally in general relativity and in our theory. An important difference occurs, however, when we consider the third observable quantity, the number of nebulae in a given magnitude class. In general relativity it is assumed that the density of nebulae was greater in the past than it is now, owing to the expansion of the universe. The theory here presented assumed that the density was the same in the past as it is now. Accordingly, if n is the number of nebulae per unit volume, the number of nebulae between r and

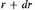
is

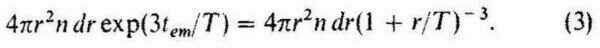
The comparison with observation consists in checking that the interdependence of the functions (1), (2), (3) is the same in observation as in theory. This process is familiar from relativistic cosmology, but there is another difference not yet referred to. In our theory the average nebular luminosity L must be constant by virtue of our fundamental assumption. This is not so in any other cosmology, where the distant nebulae, from which light reaches us only after a long time, must be assumed to have been in an earlier stage of development when the light observed was emitted. Owing to the likely variation of nebular luminosities the measurement of distances becomes very inaccurate just at the ranges where space curvature begins to be important. The theory here presented is therefore the only one which can be compared with observation without having to make any assumptions about nebular evolution.

3.3. Here Bondi and Gold argue that uncertainties in the Doppler effect corrections to observed magnitudes allow an interpretation of the number-magnitude relation in terms of the steady state theory. Under this interpretation, the observed paucity of faint nebulae is caused by a constant density of nebulae in an expanding universe; the relativistic interpretation ascribes this paucity to positive space curvature.

3.4. A difficulty which occurs in other cosmological theories is absent in ours: the problem of the time-scale. It will be useful to discuss at some length the difficulties associated with the time-scale in other theories.

The reciprocal of Hubble’s constant, which is a time (T), defined by the observations of the velocity-distance law, is between 1,800 and 2,000 million years. It is clear that this time must be of fundamental importance in any theory.

Terrestrial observations of radioactive decay in rocks indicate an age of these rocks of at least

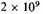
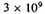
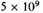
years, and some samples seem to imply an age of more than years. Astrophysical considerations tend to indicate an age of the stars in our galaxy of about years.

How do these results affect cosmology? If the continuous creation of matter is denied then the following two possibilities exist:

(i) The rate of expansion of the universe in the past was the same as now or greater. Then the origin of the universe must have been catastrophic and took place less than

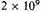
years ago. This clearly contradicts the terrestrial and astrophysical evidence referred to above. A distinction between a "dynamical" and a "cosmic" time, as suggested by Milne, removes only part of the difficulty. It makes some of the astrophysical evidence inadmissible but, since atoms and nuclei must be supposed to follow the cosmic time, the terrestrial evidence remains.

(ii) The rate of expansion was slower in the past than it is now. Then some disruptive force must have been responsible for the acceleration. Such a force is described by the hypothetical and much debated cosmological term in general relativity. A general criticism of any model based on such a disruptive force can be made, but it will be useful to discuss a special example, viz. the famous model due to Lemaître.⁹ In this model the universe is supposed to have been for an arbitrary long time in the unstable Einstein state in which λ repulsion exactly balanced gravitational attraction. The formation of condensations led to an expansion proceeding at an exponentially increasing speed.

Much more attention has been paid to the attractive formal features of this model than to the several objections to which it is open on physical grounds.

Although its past is mathematically infinite it must be taken to be entirely featureless and void of any physical development. For any physical process such as the formation of a condensation would have upset its equilibrium. In fact in its "pre-historical" state (before the first condensation) circumstances were such that the formation of a condensation was only just possible, though very unlikely, since otherwise it would have occurred earlier. However, as soon as the physical history of the model started, expansion began and so the mean density decreased. Very early on in the expansion this decrease would have been sufficient to make the previously improbable formation of condensations quite impossible. Therefore the period of physical evolution of this model is brief in spite of its infinitely long mathematical existence.

The unsatisfactory features of this model are shared by the other accelerating models of general relativity. The theory presented here differs from all these models very profoundly. Although the universe is accelerating in the sense that the speed of each particular nebula is increasing, the mean density remains constant. Therefore conditions for the condensation of new nebulae are always the same and may be taken to be always moderately favourable. The probability of the formation of condensations is presumably determined by the important non-dimensional quantity γρT². In our theory this is a constant, since all three factors are constant. (In general relativity it is variable, but in kinematical relativity it is constant, although all the factors vary.) Observations indicate that the value of this constant is between 10^-3 and 1, probably nearer 1.

Under the steady state theory the ages of nebulae follow a statistical law, and there is no reason to suppose that a particular nebula is of some age rather than another. In this theory there is therefore no difficulty in taking the age of our galaxy to be anything indicated by local observations (say

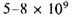
years), although the reciprocal of Hubble’s constant, T, may be much shorter.

Although this view of nebular evolution does not form an integral part of the theory, we should mention why we do not follow the view that clusters are evaporating rather than condensing. The time constant for gravitational capture is (γM/d³)^-1/2, where M is the mass of a nebula and d the internebular distance. This time is therefore only about 10¹⁰ years, compared with the period of 10¹² years required for evaporation by dynamical friction.¹⁰ Furthermore, the presence of even a very tenuous intergalactic gas would not allow nebulae to acquire the "accidentally" high velocities required for evaporation. Therefore we expect that in general the tendency for evaporation will be negligible compared with the gravitational clustering tendency.

If we assign to our galaxy, on the astrophysical evidence, an age of between

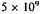
and 10¹⁰ years, it follows that there should be a moderate degree of clustering such as is actually observed.

4. THE PHYSICS OF CREATION

4.1. We shall now attempt to consider some of the details of the physical process of creation. The discussion must necessarily be somewhat speculative but some deductions can be made which limit the range of the possibilities. The average rate of creation is determined by the rate of expansion and the density of the universe¹¹ and is approximately 10^-43 g. per sec. per cm.³. We now must discuss how this creation rate is distributed in space. Will it be roughly the same everywhere or will it be very much greater in some regions than in others? In particular will it be as concentrated as the existing matter is (in which case it would be more appropriate to speak of creation per unit mass per unit time)?

The answer to this question is intimately connected with the theory of evolution. There are, roughly speaking, at present two schools of thought in this matter:

(i) One body of astronomers is of the opinion that the main line of development is centrifugal. For example, they consider that nebulae evaporate from clusters and so form the general field, that far more matter is ejected by stars than is accreted by them, so that interstellar space is populated primarily by matter which once was stellar, etc.

(ii) Another body of astronomers considers that centripetal development is predominant. In their view, accretion is far more important for stellar evolution than the ejection of matter from stars; they consider the gradual condensation of stars in the interstellar material (which is taken to constitute the bulk of the mass of a nebula) to be the main process of nebular evolution, etc.

Now it is clear from the discussion in Section 1, that in order to ensure the stationary aspect of the universe, the new material must be created in the form from which evolution starts. For, if evolution turns matter from state A into state B, then the proportion of matter in state A will be diminished unless the newly created matter is in state A. Therefore the created matter must start at the beginning of the evolutionary chain to replenish the reservoir that would otherwise dry up. Accordingly if we assume that creation is by unit mass, then we have to assume that the centrifugal line of thought is correct over an even wider field than its adherents claim, while if we assume the rate of creation per unit volume to be about the same everywhere, then we have to follow the centripetal school.

In our opinion the first view is untenable. For if matter were created mainly in the stellar interior it would have to boil off or be ejected in explosions to a distance and at a rate sufficient to supply intergalactic space with enough material for the required rate of formation of new galaxies. This implies that on an average each star loses its entire mass, by such a process of evaporation or explosion, in

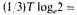
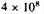
years! The known rate of occurrence of novae and supernovae shows that these phenomena can only make an insignificant contribution to this. This calculation given here does not allow for the necessary recondensation of the ejected material in its original galaxy, so that the period would be even shorter. This conclusion seems to be so absurd that we take it to prove that the rate of creation per unit volume per unit time is roughly constant and that evolution proceeds mainly in the centripetal direction. It must be clearly understood that some variation of the rate of creation is still permitted, it is only necessary that far more matter is created in space than in the stars.

Accordingly we assume that the rate of creation is everywhere about 10^-43 g. per sec. per cm.³, although variations by a factor of, say 100, are quite permissible. This rate corresponds to one new atom of hydrogen per cubic metre per

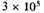
years. Accordingly we cannot expect the process to be directly observable.

4.2. We have seen that the process of creation will take place everywhere and that most of the matter will be created in the vast intergalactic spaces. The next question to engage our attention will be the initial motion of the created matter.

It is evident that this velocity associated with creation cannot be relativistically invariant, nor can invariance be introduced by assuming a random distribution of velocities, since the only invariant distribution diverges.

It follows, therefore, that there will be a preferred time-like direction at each point of space-time, and that the initial motion of newly created matter will be either along this direction (in the 4-dimensional sense) or will be distributed about it in a non-invariant way. The question of this distribution will be discussed later; for the moment it will be assumed that the matter is actually created along the preferred direction.

The adoption of a non-invariant law of creation may at first sight seem surprising; but are we entitled to demand invariance of creation when the resulting movement of matter is well known not to be invariant? Even in the cosmologies of general relativity the existence of a preferred direction is explicitly recognized in Weyl’s postulate. General relativity demands that the laws of cosmology should be invariant while admitting that the one and only application is not invariant. We can see no reason why the laws of nature determining the structure of our universe should be invariant, although the universe is unique and does not bear an invariant aspect.

The identification of the preferred direction defined by the creation of matter with the preferred direction defined by the motion of matter (as discussed in 2.4) is compelling. It is most satisfactory that our theory can connect the direction defined everywhere by the motion of matter with another phenomenon, while in other theories no such connection exists.

It should be realized that the existence of this preferred state of motion not only conflicts with general relativity, but also with restricted (and even with Galilean) relativity. However, this lack of invariance is nothing new. As we have seen in Section 2 it is an immediate consequence of the law of the recession of nebulae.

4.3. We must now consider the problem of the probability distribution of the initial velocity about the preferred direction. If the spread of velocities were great, then this would lead either to large amounts of radiation from intergalactic space or to high temperatures of intergalactic matter.

The amount of radiation observed and the postulated intergalactic condensation limit the velocity spread to at most 10⁷ cm./sec., corresponding to a temperature of at most 50,000 deg.

There do not seem to be any arguments setting a lower limit to the temperature and the arguments limiting the temperature from above all depend on the absence of any effects of the temperature. If one wishes to have a definite and simple picture of the process, one can therefore assume that matter is created without random velocities (i.e. at zero temperature). although this is not a necessary conclusion.

4.4. The next question we must discuss is the electric charge of the created matter. Now it is clear that an average excess charge of either sign would lead to forces of repulsion tending to remove the excess charge to infinity. The speed with which the excess charge is repelled to infinity depends on the ratio of excess charge to mass. It can be shown¹² that if this ratio is greater than about

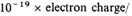
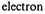
mass, then this repulsion of excess charge would take place at a speed greater than the speed of expansion of the material universe. But such a rapidly "expanding universe of excess charge" cannot be present together with a slowly expanding "universe of matter" without violating the principle of homogeneity. Accordingly we can conclude that if there is any average charge excess of the created matter, the average charge-mass ratio must not exceed the very low limit mentioned above.

These results give us some indication of what the created matter may be. If we reject as far-fetched the possibility of the creation of dust, etc., and concentrate on the simplest building material, then we are left with the following possibilities:

(i) Protons and electrons, created separately but at identical (or very nearly identical) rates. The radiation arising from collisions or captures would be just within the limits laid down in 4.3.

(ii) Neutrons. The energy released by the disintegration of the neutrons would (within a few hours of creation) lead to velocities and radiation somewhat in excess of the limits mentioned. Nevertheless, this possibility is so attractive that it should not be ruled out without further examination.

(iii) Hydrogen atoms.

The last possibility seems to agree best with the view adopted in 4.3, although (i) cannot be excluded. Since (i) would, but for the necessarily small amount of radiation, also lead to the formation of hydrogen in the ground state, we can for simplicity and definiteness adopt (iii).

In agreement with the widely held view that the building-up of the elements is a complex stellar process and that the traces of elements other than hydrogen in interstellar space are due to explosion and ejection of matter from stars, we have assumed here that all matter starts its career as hydrogen. This seems to us to be very plausible, but is a separate subject not directly connected with the creation theory.

4.5. We finally have to consider where in space-time matter is created and it seems to be most reasonable to assume that it is created in a random manner. According to this view the probability of creation taking place in any particular fourdimensional element of volume (spatial volume

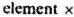
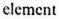
of time) is simply proportional to its (fourdimensional) volume, the factor of proportionality being a function of position.

By our argument in 4.1 this factor cannot vary very much from point to point.

Accordingly randomness would be introduced by the random origin of particles, but not necessarily by any initial random motion.

5. THE FUNCTION OF A FIELD THEORY

Here Bondi and Gold argue that a new field theory must be developed and that in their view the general theory of relativity is inadequate. They also find Hoyle’s¹³ adaptation of general relativity to the steady state situation unsatisfactory and unacceptable. The theory of general relativity is unacceptable because it requires conservation of mass, and both the general relativity theory and Hoyle’s adaptation are unacceptable because they violate Mach’s principle.

1. In 1926 Edwin Hubble provided some observational evidence in support of the cosmological principle, when he professed to show that the distribution of galaxies is spatially homogeneous and isotropic (see selection 105). Although some of Hubble’s number counts have been subsequently discredited, the galaxies do seem to be homogeneously and isotropically distributed when sufficiently large regions are observed.

2. F. Hoyle, Monthly Notices of the Royal Astronomical Society 108, 372 (1948).

3. F. Hoyle, Nature 208, 111 (1965).

4. Selections 13 and 132. Also see F. Hoyle and R. J. Tayler, Nature 203, 1108 (1964), and R. V. Wagoner, Astrophysical Journal 179, 343 (1973).

1. E. Mach, The Science of Mechanics (London, 1893), pp. 229–238.

2. H. Weyl, Phys. Z. 24, 230–232 (1923); Phil. Mag., ser. 7, 9, 936–943 (1930).

3. Olbers, Bode’s Jahrbuch 10, 1826.

4. A. S. Eddington, Proc. Roy. Soc. A 133, 605 (1931); M.N. 92, 3 (1932).

5. H. P. Robertson, Ap. J. 82, 284 (1935).

6. A. G. Walker, Proc. Lond. Math. Soc., ser. 2, 42, 90 (1936).

7. W. de Sitter, Proc. Akad. Wetensch. Amst. 19, 1217 (1917).

8. H. P. Robertson, Rev. Mod. Phys. 5, 71 (1933).

9. G. Lemaître, M.N. 91, 483 (1931).

10. M. Tuberg, Ap. J. 98, 501 (1943).

11. Cf. E. Hubble, The Realm of the Nebulae (Oxford, 1936), p. 189.

12. Unpublished theorem of Newtonian Cosmology.

13. F. Hoyle, M.N. 108, 372 (1948).