On Dense Stars
Ralph Howard Fowler
(Monthly Notices of the Royal Astronomical Society 87, 114–122 [1926])
1. INTRODUCTION
THE ACCEPTED DENSITY of matter in stars such as the companion of Sirius is of the order of 105 gm./c.c. This large density has already given rise to most interesting theoretical considerations, largely due to Eddington. We recognise now that matter can exist in such a dense state if it has sufficient energy, so that the electrons are not bound in their ordinary atomic orbits of atomic dimensions, but are in the main free—with sufficient energy to escape from any nucleus they may be near. The density of such "energetic" matter is then only limited a priori by the "sizes" of electrons and atomic nuclei. The "volumes" of these are perhaps 10-14 of the volume of the corresponding atoms, so that densities up to 1014 times that of terrestrial material may not be impossible. Since the greatest stellar densities are of an altogether lower order of magnitude, the limitations imposed by the "sizes" of the nuclei and electrons can be ignored in discussions of stellar densities, and the structural particles of stellar matter can be treated as massive charged points.
Eddington has recently1 pointed out a difficulty in the theory of such matter. Assuming it to behave more or less like a perfect gas, modified by its electrostatic forces and the sizes of such atomic structures as remain undissolved, there is a perfectly definite relation between the energy and the temperature, which depends on the density only to a minor degree. This assumption even here is not so unreasonable as appears at first sight. But even without it we naturally expect a perfectly definite relation between energy and temperature, in which there is a close correlation between large energies and large temperatures, small energies and small temperatures. The emission of energy by the star will proceed in the usual way at a rate depending on the surface temperature, and the internal temperatures must provide the gradient necessary to drive the radiation out. So long as the star contains matter at a high temperature, radiation of energy must presumably go on. But then, according to Eddington, there may come a time when a very curious state of affairs is set up. The stellar material will have radiated so much energy that it has less energy than the same matter in normal atoms expanded at the absolute zero of temperature. If part of it were removed from the star, and the pressure taken off, what could it do?
The present note is devoted to a further consideration of this paradox. It is clear that the crucial point is the connection between the energy and the temperature. In a sense the temperature measures the "looseness" of the system, the number of possible configurations which it can assume, and therefore its radiation. These depend directly on the temperature, and only on the energy in so far as the energy determines the temperature. The excessive densities involved suggest that the most exact form of statistical mechanics must be used to discuss the relationship between the energy, temperature, and density of the material. This is a form suggested by the properties of atoms and the new quantum mechanics, which has been already applied to simple gases by Fermi and Dirac.2 It may be accepted now as certain that classical statistical mechanics is not applicable at extreme densities, even to ideal material composed of extensionless mass-points, and that the form used here is fairly certainly the correct substitute. Its essential feature is a principle of exclusion which prevents two mass-points ever occupying exactly the same cell of extension h3 of the six-dimensional phase-space of the mass-points. When this form of statistical mechanics is adopted, it at once appears that the suggested difficulty resolves itself, and there is really no difficulty at all. The apparent difficulty was due to the use of a wrong correlation between energy and temperature, suggested by classical statistical mechanics. When the correct relation is substituted, it is found that the limiting state of such dense stellar matter is one which the energy is still, as it must be, excessively great, but the temperature is zero! Since the temperature determines the radiation, radiation stops when the dense matter has still ample energy to expand and form normal matter if the pressure happened to be removed. As the dense matter radiates its energy away, the number of its possible configurations rapidly falls, and therewith the temperature. The absolutely final state is one in which there is only one possible configuration left. Temperature then ceases to have any meaning, for the star is strictly analogous to one gigantic molecule in its lowest quantum state. We may call the temperature then zero.
Whether or no some such explanation may not be equally possible using other forms of statistical mechanics (perhaps the classical) I am not prepared to say. The new form used here seems for entirely independent reasons so satisfactory that its applicability need not be questioned. On application it clears up Eddington’s question in a convincing manner, and I am content to leave the matter so.
2. THE EQUILIBRIUM STATE OF DENSE MATTER
It is obviously reasonable to consider dense stellar material as an assembly of free electrons and bare nuclei of net charge zero. It is, however, necessary to idealise the problem a little further and ignore the electrostatic charges, so that the whole energy of the assembly is the kinetic energy of translation of the various particles. We shall later see reason to believe that this idealisation does not vitiate the results, or at least not their qualitative form, for we are really mainly concerned with calculations of amounts of phase-space, and these are independent of potential energy.
Consider a volume V of stellar material consisting of N/q bare nuclei of mass mq and N free electrons of mass m, with total (kinetic) energy E. We will assume as a first approximation, as we have said, that the electrostatic forces may be ignored, and then that the statistics of assemblies of practically independent systems is applicable. Then3 the total number of complexions C representing any state of the assembly is
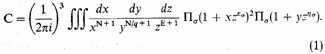
In this equation
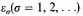
are the possible energies of an independent electron in a volume V, and
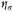
those of an independent nucleus. The power 2 enters because the electron has a structure (axis of spin) which gives it two possible orientations in a magnetic field, that is, a statistical weight 2. The nucleus probably also has a weight greater than unity, but the nuclear terms turn out to be unimportant, so that we need not spend time over this refinement. Students of classical statistical mechanics will recall that the classical formula differs from this only in having
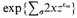
in place of
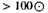
All the mean values associated with the equilibrium state of the assembly can be derived from C, and the value of C can be obtained by "steepest descents." Writing
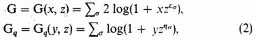
the critical value of the integrand is determined by the unique root λ, μ, θ of the equations
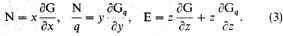
With these special values of x, y, z we have, among other equations,
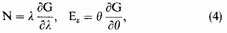
where
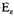
is the average energy of the free electrons. Also
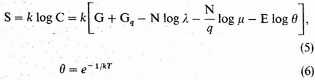
The number of possible energy values for an electron of mass m in a volume V which lie between τ and
is
4

Therefore
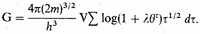
The values of
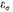
are extremely closely spaced, so that for a fixed value of
θ we can replace the sum by an integral with negligible error and find
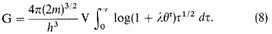
Strictly we shall want to make
The form (8) might then fail, but as we shall really not be interested in the differences between
or even
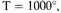
this does not matter, and we shall assume the general validity of (8). The validity of some applications of (8) can be checked in the limit by direct calculation. N and
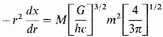
are obtained from this by differentiation. Similar forms and equations hold for G
q, N/
q, and E
q for the nuclei. The assembly is a thermodynamic system.
Our chief interest is now to trace the series of equilibrium states of such an assembly as its energy is slowly radiated away. A loss of energy by radiation means necessarily a loss of entropy, and therefore a fall of temperature. We have therefore to trace the behavior of the assembly as θ decreases—presumably as
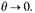
But by (4) and (8) N depends on a function of the form
If λ has an upper bound b, this is less than
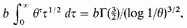
and therefore tends to 0 as
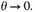
This would make
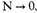
which is impossible, as the number of particles is fixed. Since
λ cannot have an upper bound, it is reasonable to assume that

We shall see shortly that this is a necessary consequence of
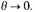
Let us therefore write
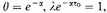
defining
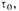
and assume that
λ and therefore
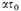
are large. Then
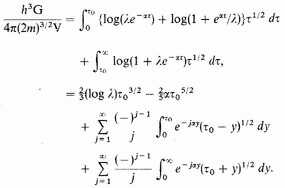
In transforming the integrals we have used the fact that
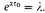
Since
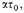
and
a fortiori
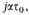
are large, we have approximately
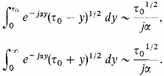
Therefore finally (and approximately)
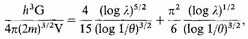
an equation whose real value can be expressed in the form
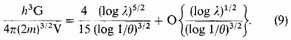
This equation can be differentiated. Therefore
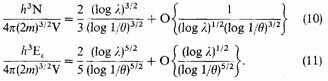
It follows from (10) that
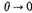
implies
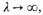
and therefore from (10) and (11) combined that as
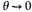
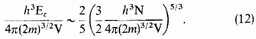
The temperature can (and presumably would) fall to zero, still leaving, however, the free electrons with kinetic energy
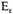
given by (12). Similar relations hold for the nuclei. In the limit, however,
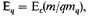
and is therefore negligible compared with
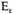
.
It is wise to check up the behaviour of the entropy meanwhile. The contribution
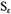
by the electrons is given by
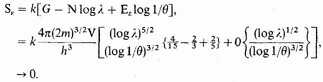
The contribution by the nuclei behaves in a similar way. This is correct.
We may note that the relation (12) can be confirmed by a direct calculation of the tight-packed phase-space required to house the N electrons. If the number of cells is the number of electrons, we find from (7)
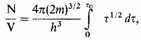
while at the same time
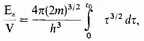
which together give (12).
3. NUMERICAL CALCULATIONS
Let us assume that the density of the stellar matter is 10x gm./c.c., and that it is composed on the average of iron atoms, at
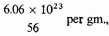
or
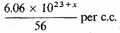
Then for the free electrons,
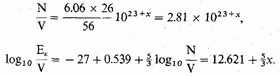
For density 105 gm./c.c.
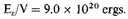
Thus the average kinetic energy of an electron in this state is
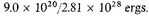
This is the same as the average kinetic energy of an
electron in an expanded gas at a temperature T, where
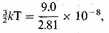
or
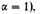
It is not, however, possible to rest quite content with this result, since the electrostatic energy terms are far from negligible, and in fact of the same order of magnitude. We observe first that the equation (12) is based entirely on considerations of phase-space. There must be enough cells of extension h3 in six-dimensional phase-space to accommodate all the electrons. The phase-space depends only on velocities, or kinetic energy of the electrons, and is independent of the potential energy terms. The relation (12), therefore, should continue to give the necessary kinetic energy of the electrons, at least reasonably accurately, even when the effects of potential energy are allowed for. We have therefore merely to attempt to estimate the negative potential energy in order to compare the total energy of the condensed matter with its total energy in an expanded form.
The negative potential energy of a normal atom can be estimated roughly but easily if we recall that the average negative potential energy of an orbit in an inverse square field is twice the negative (total) energy of the orbit. The total negative energy of an iron atom is5
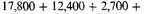
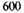
volts for the K, L, M, and N electrons respectively, or 33,500 volts in all. The negative potential energy of one atom may therefore be taken to be
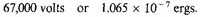
The negative potential energy of the atoms equivalent to 1 c.c. of density 10x is therefore
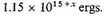
For the standard case of density 105 the negative energy of the normal atoms is, therefore, say 1020 ergs.
The negative potential energy in the condensed form is far more difficult to estimate with any pretence to accuracy. If we simply say that at a density 10x everything will on the whole be about
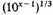
closer than it could be packed before in normal atoms, we might argue that the negative potential energy would be increased about
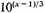
times, and so become
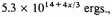
or in the standard case
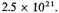
This, however, must grossly over-estimate the increase. For half the negative energy comes from the two K electrons normally at a distance of
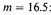
from the nucleus. The average distance of uniformly distributed electrons at a density 10
5 is as much as
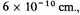
and there is no reason for two electrons on the average to sink into about
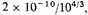
that is 10
-11 cm. They might be expected to get hardly any closer, and the L-electrons not to experience the full shrinkage. If the contribution of the two electrons corresponding to the K electrons is unaltered, the potential energy increase, and therefore roughly the potential energy, is halved, and the incomplete shrinkage of the L group would halve the energy again. A negative potential energy of
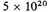
is all that can be expected.
An alternative estimate may be made as follows. The average space assigned to each nucleus is a sphere of radius r0, where
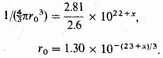
Let us estimate the electrostatic energy by distributing 26 electrons uniformly between ο and r0 for each nucleus, assume that the field of a single point charge 26e acts on each and ignore their own repulsions. Such an average distribution is not far wrong, for it is known that there is comparatively little crowding of bound electrons owing to the quantum restrictions, or of free electrons owing to the energy conditions.6 Thus the negative energy per atom is
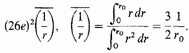
The negative potential energy per c.c. of condensed matter is therefore
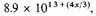
or in the standard case
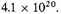
All this is very uncertain; the best we can do is to conclude that the negative potential energy of the condensed form is about
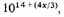
or in the standard case
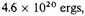
compared with 10
20 ergs when expanded in normal atoms. As a result the kinetic energy is perhaps twice the negative potential energy for a density 10
5, and the expanded form could become a perfect gas of normal
atoms at about
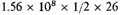
say
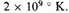
Whether or no by our rough calculations we can show that the total energy of the condensed form is large and positive for a density of 105, we can certainly conclude that this must be true for still greater densities, for the kinetic energy per unit volume varies as 10(5x/3), and on almost any view the negative potential energy must vary ultimately like 10(4x/3). There seems no reason to doubt that this inequality, kinetic energy greater than negative potential energy, is true over wider conditions than we can show by these arguments. For in condensed forms at somewhat lower densities the tight packing is presumably achieved at the expense of shifting only the more lightly bound electrons, and our estimates of increase in the negative potential energy will be greatly in excess.
4. COGNATE SPECULATIONS
If we return to the condensed assembly of mass-points, electrostatic forces ignored, we may note that the pressure is given by the thermodynamic equation
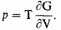
This is strictly the pressure exerted by the electrons, and obeys the usual perfect gas equation
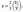
the contribution by the nuclei is trivial by comparison. Thus in the condensed limit
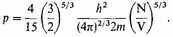
If the volume is a sphere of radius R, then
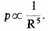
This pressure represents an interaction of the assembly with the outside world which is in a sense due to the quantum restraints to which the assembly is subject.
Now an atom, especially an atom of an inert gas, is really condensed matter of just the same general type. The assembly, whether atom or stellar material, contains just so many cells of phase-space available for electrons and every one of them is full. It is tempting to speculate as to whether the apparent forces of repulsion, which prevent the too close approach of atoms, molecules, or ions with closed configurations of electrons, may not be due in just the same way purely to the quantum constraints. The number of cells of the phase-space must be unaltered in an encounter, and the apparent force of repulsion represents just the work which must be done to make up by an increase in the velocity (or kinetic energy) space for a loss in the extent of the "space"-space. These forces of repulsion between condensed atomic configurations of electrons seem empirically to vary like 1/R10, or there-abouts, for a large variety of atoms. It would be too much to expect the pressure of the stellar material to follow exactly the same law. But the general forms of the two types of system are sufficiently alike, and the resemblance of their laws of interaction close enough to lead one to believe that the origin of this important part of inter-atomic forces is to be sought in this direction, in the quasi-thermodynamic consequences of the existence of the quantum constraints embodied in Pauli’s principle.
1. E. C. Stoner, Philosophical Magazine 7, 63 (1929), 9, 944 (1930); W. Anderson, Zeitschrift für Physik 54, 433 (1929).
2. S. Chandrasekhar, Astrophysical Journal 74, 81 (1931), Monthly Notices of the Royal Astronomical Society 95, 207, 226, 676 (1935), and An Introduction to Stellar Structure (Chicago: University of Chicago Press, 1938).
1. Eddington, The Internal Constitution of the Stars (Cambridge Univ. Press, 1926), §117.
2. Fermi, Rend. Acc. Lincei, Ser. 6, 3, 145 (1926); Dirac, Proc. Roy. Soc. A 112, 661 (1926). See also Fowler, Proc. Roy. Soc. A 113, 432 (1926), for a full account with other references.
3. The following formulæ will be found in detail in Fowler.
4. Dirac, p. 671.
5. Hartree, Proc. Camb. Phil. Soc. 22, 464 (1924).
6. For the latter see Eddington, §183.