Harlow Shapley "On the Nature and Cause of Cepheid Variation," Astrophyical Journal 40 105–122 1914
The Pulsation Hypothesis
By Harlow Shapley
INTRODUCTION
The purpose of the present discussion is an attempt to investigate the question of whether or not we should abandon the usually accepted double-star interpretation of Cepheid variation. In addition to the brief statement of some general considerations and correlations of the many well known characteristics of Cepheid and cluster variables, certain recently discovered properties of these stars are discussed in greater detail, because chiefly upon them are based the conclusions reached in this study.
It seems a misfortune, perhaps, for the progress of research on the causes of light-variation of the Cepheid type, that the oscillations of the spectral lines in nearly every case can be so readily attributed, by means of the Doppler principle, to elliptical motion in a binary system. The natural conclusion that all Cepheid variables are spectroscopic binaries has been the controlling and fundamental assumption in all the recently attempted interpretations of their light-variability, and the possibility of intrinsic light-fluctuations of a single star has received little attention.
From the very first there have been serious troubles with each new theory. Considered from the spectroscopic side alone, the Cepheids stand out as unexplainable anomalies. There are persistent peculiarities in the spectroscopic elements, such as the low value of the mass function, the universal absence of a secondary spectrum, and the minute apparent orbits. Practically the only thing they have in common with ordinary spectroscopic binaries is the definitely periodic oscillation of the spectral lines, which permits, with some well known conspicuous exceptions, of interpretation as periodic orbital motion. Adding, then, to the spectroscopic abnormalities the curious relations between light-variation and radial motion, the difficulties in the way of all the proposed simple solutions seem insurmountable. Geometric explanations of the light-variation fail completely, and little better can be said of the hypotheses that involve partly meteorological and partly orbital assumptions.
The writer can offer no complete explanation of Cepheid variability as a substitute for the existing theories that are shown to be more and more inadequate. At most, only the direction in which the real interpretation seems to lie can be pointed out, and an indication given of the strength of the observational data that would support the theory developed along the lines suggested. The principal results of a rather extensive investigation, further details of which it is hoped can be published in subsequent papers in the near future, are outlined in the following paragraphs. The main conclusion is that the Cepheid and cluster variables are not binary systems, and that the explanation of their light-changes can much more likely be found in a consideration of internal or surface pulsations of isolated stellar bodies.
THE ESSENTIAL IDENTITY OF CEPHEID AND CLUSTER VARIABLES
The subdivision of the short-period variables into the cluster type and the Cepheid is an artificial one. This proposition scarcely needs proof, although the assumption of the essential similarity of the two groups is important in the following discussion. Practically all writers on the subject are more or less inclined to accept this view. The definition of the cluster-type variable is, in fact, by some merely "short-period Cepheid." Others, including Hartwig and Kron, have considered only those with rapidly decreasing brightness and constant light at minimum as "antalgol" or cluster-type variables. Kron calls the shortest-period variable known [at that time, XX Cygni, period 3h 14m] a Cepheid, and Hertzsprung designates as Cepheids only those variables whose periods are greater than a day. The writer proposes to adopt, merely as a convenience, the latter practice, arbitrarily calling the Cepheids of periods less than a day cluster-type variables; for there is at present no evidence of real difference between the two classes in the nature or probable causes of the light and velocity variations. Hertzsprung calls attention to the maxima in the frequency-curve of the periods at twelve hours and at seven days, and notes also that the longer-period Cepheids are in the galaxy, while the shorter-period Cepheids or cluster variables are apparently distributed more at random over the sky. Making the reasonable assumption that the data, though rather meager, are sufficient, nevertheless, to establish the reality of both phenomena, these conditions do not impeach the hypothesis that the light and velocity variations of the long- and short-period Cepheids are attributable to the same causes, and that the only modifications necessary in an explanation of one, to make it applicable to the other, are those depending on the length of the periods and other gradative characteristics, such as differences of spectral type and relative speed of light-change at corresponding phases. Among the several arguments that tend to prove the inherent similarity of the two groups of Cepheids, the following are the most important.
a) For RR Lyrae, period 13.6 hours, which is commonly classified as a cluster-type variable, the spectroscopic orbit by Kiess resembles in all details the peculiar orbits characteristic of the longer-period Cepheids. The light-curve is typical of cluster variables in all its properties.
b) From the photometric standpoint, Graft and Bottlinger have found no essential differences between light-curves of cluster and Cepheid types, and insist on the artificiality of the division into two classes. Very few, if any, of the cluster-type variables have rigorously constant light at minimum phase, as Plummer, among others, has shown. In fact, it was partly for this reason that Hartwig abandoned, in the Vierteljahrsschrift catalogue, the former term "antalgol" and the former distinction between cluster and Cepheid variables.
c) Russell’s harmonic analyses of the mean light-curves of typical cluster variables and typical Cepheids indicate the necessity of analogous interpretations of the two.
d) An unpublished investigation by the writer of the relation between the periods and spectral types of all variables shows the existence of a continuous property from the longest-period Cepheids to the shortest-period cluster variables.
e) The shift of the maximum intensity in the spectra toward the violet with increasing light is a property common to both classes.
[Here follows a discussion of the irregularities in the period-length of Cepheid variables and irregularities in their light-curves, presented as arguments against the binary hypothesis.]
CHANGES IN COLOR AND SPECTRAL TYPE
A third argument against the binary interpretation of Cepheids is the difficulty such theories would have in explaining the periodic change of the spectral type, though it must be admitted that to a certain extent Duncan’s hypothesis, if otherwise acceptable, could account for spectral changes through the medium of atmospheric absorption. The evidences of the change of spectral type with changing light, though not well known nor generally recognized, are decisive and important. Schwarzchild, Wirtz, and more particularly Wilkens have demonstrated for Cepheids of longer period that the range of light-variation is greater in the photographic than in the visual part of the spectrum. The photographic work of Martin and Plummer suggests similar results for cluster-type variables, while recent simultaneous photographic and photovisual observations by Mr. Seares and the writer at Mount Wilson establish the fact definitely. The shift of the maximum intensity in the spectra of Cepheids, discovered by Albrecht, has been confirmed by Kiess and other Lick observers. These two factors—the greater photographic range and the shift of the maximum intensity—would suggest as an underlying and common cause a change in the spectral type. Albrecht and Duncan have observed that Wright’s spectrograms of η Aquilae suggest a later type of spectrum at minimum than at maximum. The Harvard classification of TT Aquilae at maximum is G, at minimum, K.
For the cluster-type variables there is more direct evidence of distinct and continuous change. At the writer’s request Miss Cannon has examined some of the Harvard spectrograms of certain cluster variables. For RR Lyrae no definite change was recorded on the plates examined, and similarly for XZ Cygni, but the spectrum, when faint, was extremely uncertain. For SW Andromedae the spectrum was of type A at maximum and dearly of a redder type at minimum. The most conclusive results, however, are obtained from the series of spectrograms taken by Mr. Pease in July of this year with the 60-inch reflector of the Mount Wilson Observatory. The variable RS Bootis, period 9h.1, shows a continuous change of spectral type from F0 at minimum to B8 at maximum. One consequence of this result is that hereafter the classification of all Cepheid and cluster-type spectra must be made with due specification of the corresponding phase of light-variation. Another difficulty in the spectral changes, that must not be overlooked in attempting a complete explanation of the Cepheid phenomena, is a peculiarity observed by Albrecht on his plates of Y Ophiuchi and T Vulpeculae. Various lines showed large irregular shifts, which are not progressive with the phase of the star in its light-period.
CONCERNING EXISTING HYPOTHESES
The fourth principal argument against the binary interpretation of Cepheids is the inadequacy of all the existing double-star hypotheses. To many this is not only the best argument but is sufficient in itself. A
detailed criticism of these attempted explanations is unnecessary, for this has been generously provided by the proposers of the theories themselves, as well as by others, including Campbell, Plummer, Brunt, Kiess, and Ludendorff. There is one point, however, that has not been considered, which is of prime importance in the discussion of Cepheid phenomena. Russell and Hertzsprung have independently shown that the Cepheids are stars of small peculiar motions and small parallaxes, and hence of great absolute brightness. The former finds a mean absolute magnitude of -2.4 and the latter of -2.3, that is, the average Cepheid (the spectrum is of solar type) is nearly 700 times as bright as the sun. It is reasonable to assume that the Cepheids and the sun have a comparable surface brightness. The average Cepheid, then, has a volume between fifteen and twenty thousand times as great as that of the sun.
Interpreted as spectroscopic binaries these giant stars move in orbits whose apparent radii average less than one-tenth the radii of the stars themselves. In order that the radii of the real orbits may greatly exceed those of the apparent orbits, the inclinations must be very small, a condition which cannot be supposed to exist generally for Cepheid orbits. The difficulty in applying the hypotheses of Eddie, Loud, Duncan, and Roberts is therefore immediately apparent. Moreover, if the mass of the average Cepheid is admitted to be as much as five times the solar mass, the density is still astonishingly low—hardly three ten-thousandths that of the sun. Considering the low average value of the mass function derived from the orbits of the Cepheids, and taking a random distribution of the orbital inclinations, the non-luminous second body, to which Duncan’s theory assigns the extensive atmosphere that must envelope the giant primary, has about one-tenth of the mass and therefore must move with an average apparent orbital velocity of about 200 km a second. Remembering the size of the primary star compared with its orbit, we know that the mass of the secondary must be still smaller and the velocity higher to separate the stars.
A SUGGESTED EXPLANATION OF CEPHEID VARIATION
In the face of all these difficulties, it seems appropriate to abandon completely the attempts to interpret Cepheids on the basis of a binary-star assumption. It has been shown by Russell that the light-variations cannot be explained satisfactorily by the uniform rotation of a single spotted star; the light-change must be intrinsic, and not just apparent. The explanation that appears to promise the simplest solution of most, if not all, of the Cepheid phenomena is founded on the rather vague conception of periodic pulsations in the masses of isolated stars. The vagueness of the hypothesis lies chiefly in our lack of knowledge of the internal structure of stellar bodies, and not in the difficulty of explaining the observed facts if once we assume the stars to be ideally gaseous figures of equilibrium. Moulton has considered the matter of explaining certain types of stellar variation from this point of view, but his conclusions are scarcely applicable to Cepheid variables in the light of our present knowledge of their peculiar properties. According to him, the light-change should be due to the heat generated by the oscillation of a spherical star from an oblate to a prolate form, there being a maximum of light-emission every time the star passes through its mean spherical figure. The period of velocity variation, then, should be double that of the light-change, and this, of course, does not conform with known conditions. It is to this phenomenon of pulsating stellar masses, however, that the writer would ascribe the light and velocity variation of Cepheid and cluster variables, and the theoretical work of Moulton, Jeans, Emden,1 and others on the properties of gaseous spheres already justifies the conclusion that such oscillations are both possible and probable. They might arise, as Moulton suggests, from the collision with masses of only planetary dimensions, from the near approach of two stars, or in other ways.
Without any pretense of explaining clearly or fully on this hypothesis all the properties of Cepheid variation that have given the double-star theories such hopeless difficulty, a few points favoring the pulsation suggestion will be summarily stated. There will exist originally, as the result of the initial disturbance, a great number of oscillations of different periods. The character of these various vibrations will depend on the nature of the stellar structure. For the ideal homogeneous fluid mass investigated by Kelvin, and for the polytropic gaseous sphere defined and studied by Emden, the period of vibration of each type is independent of the volume and mass and depends only on the mean density and the order of the harmonic term defining the oscillation. For any given mean density the most important oscillation is that corresponding to the second-order harmonic. Its period is the longest, its amplitude the greatest, and it may persist with inappreciable change in period almost indefinitely, while the oscillations of higher order are more rapidly destroyed by friction.
If, then, we attribute the principal light-change in a Cepheid variable to this principal oscillation, and if we are willing to adopt Emden’s polytropic gaseous sphere as a stellar model, we can compute at once the density of each individual variable. Obtained in this way the densities are probably of the right order of magnitude, whatever function of the radius, within reasonable limits, the density is assumed to be; and for an incompressible homogeneous fluid they would be only 2.5 times as large. The densities in terms of the sun for all the Cepheids of known periods and spectra have been derived in this manner, with the results given in Table I.
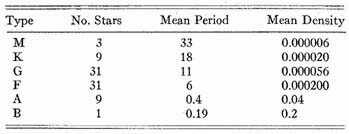TABLE I
The extremely low densities for the Cepheids of the redder spectral types until recently might have thrown serious doubt on the hypothesis that demands such abnormally low values. But now for two reasons we are ready to accept as possible these supposedly impossible densities. In the first place, as Hertzsprung has pointed out in his proof that the Cepheids of solar spectral type are giant stars, the average mean density must be of the order of
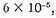
if the masses are comparable with that of the sun. They may be larger, but from our knowledge of stellar masses in general we are inclined to believe that they are not more than ten times that of the sun, which is sufficient to prove the point. In the second place, the densities of several long-period eclipsing binaries of types G and K are now available for comparison. For instance: RX Cassiopeiae, type KO, means density
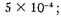
W. Crucis, type Gp, mean density
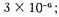
SX Cassiopeiae, type G3, mean density
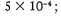
RZ Ophiuchi, type F8, density of one component 10
-3. For the A- and B-type spectra, the Cepheid densities are, of course, entirely normal compared with eclipsing star densities.
As previously stated, the Cepheids without doubt are enormously large. Their small observed velocity variations, even if attributed altogether to motion in the line of sight and not at all to pressure-shifts, are not larger than might arise from a radial oscillation through but a small fraction of their mean diameters. In the central mass of the star the period of the supposed pulsation should, of course, be perfectly regular, but its effect need by no means be regular on the radiating surface.
We may suppose that, because of the internal vibration, the photosphere of the star is periodically scattered or broken through by the rush of hotter gases from the interior. Maximum light and maximum velocity of approach would obviously be approximately synchronous, and their coincidence would naturally be independent of the direction of the observer in space. Ludendorff’s correlation of range of light and range of velocity is highly significant in this connection. The essentially harmonic nature of the oscillation at the surface of the star would easily lend itself to interpretation as elliptic motion, though non-elliptic motion need not be unexpected, nor the anomalous behavior of certain spectral lines. In stars in which the initial disturbance is of recent origin, the presence of secondary oscillations could be expected, which would affect the light as well as the velocity.
It should be noted as an important factor in the explanation of Cepheid variation, that a change in the spectrum of a given radiating surface from one type to the next will change the visual brightness of that surface by approximately one stellar magnitude, and the color range by four-tenths of a magnitude. These quantities correspond very closely to what is observed in cluster variables, and suggest that, if desired, it is unnecessary to go farther for the explanation of the light-variation than to suppose that a surface of approximately constant area progressively changes its spectral type as the result of a periodic flow and ebb of heat. That the light-change should be of a more explosive character for the cluster-variables than for the longer-period Cepheids would be expected because of their higher mean densities.
Various other details suggesting the possibility of the above interpretation could be cited,2 but this sketch of the pulsation argument will suffice for the present, since the purpose of the paper is not so much to advance an alternative theory as to question the validity of the spectroscopic binary hyothesis.
1 [In this regard R. Emden’s Gaskugeln (Teubner, Leipzig, Berlin, 1907) is significant, especially the paragraphs under "Die Pulsierende Sonne."]
2 [For the first theoretical development of the pulsation hypothesis see papers by A. S. Eddington in the Monthly Notices, Roy. Ast. Soc. 79, 2-22 (1918); 79, 177-188 (1919); see also 101, 182-194 (1941).]